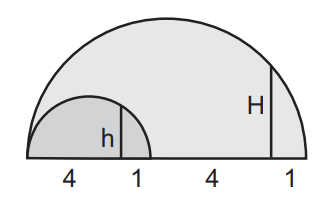
(CESGRANRIO) A figura abaixo representa duas semicircunferências de diâmetros 5 e 10, respectivamente. Os dois segmentos perpendiculares aos diâmetros indicados na figura têm medidas h e H.
- 1958041-20211011114344000000-0.png (12.11 KiB) Exibido 243 vezes
O valor numérico da razão [tex3]\frac{H}{h}[/tex3]
é
A) [tex3]\frac{9}{2}[/tex3]
B) [tex3]\frac{9}{4}[/tex3]
C) [tex3]\frac{10}{5}[/tex3]
D) [tex3]\frac{3}{2}[/tex3]
E) [tex3]\frac{3}{4}[/tex3]

