|
Com a idéia básica vista nos dois capítulos anteriores podemos dar mais um passo. Agora sim em direção a uma matéria que já pode ser cobrada no vestibular (ah, mas mesmo a matéria anterior não sendo cobrada diretamente, é necessário sabê-la para compreender esta aqui e as posteriores).
Lembrando que o logaritmo é um expoente, podemos enunciar a equivalência fundamental dos logaritmos:
| EQUIVALÊNCIA FUNDAMENTAL |
|
Note que temos, na expressão acima, exatamente as duas maneiras de mostrar a pergunta feita no início do estudo de logaritmos: "Qual o expoente x que devemos elevar a base b para
resultar N". |
Esta equivalência é muito
importante, pois muitos exercícios sobre logaritmos necessitam dela para sua resolução.
Veja, que, a flecha indicada nessa propriedade está nos dois sentidos, ou seja, você
pode transformar logaritmo em exponencial e exponencial em logaritmos.
Vamos dar um exemplo de cada:
Ex. 1 - Qual o logaritmo de 216 na base 6?
Em outras palavras, podemos escrever esta
pergunta como:
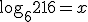
Onde x é o valor procurado, ou seja, o
logaritmo elucidado no enunciado.
Agora, para resolver, aplicamos a
equivalência fundamental:
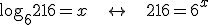
Caímos em uma exponencial, para resolver
devemos igualar as bases (como visto na lição anterior). Fatorando o  . .
 Cortando as bases Cortando as bases
 Portanto, log6 216 = 3 Portanto, log6 216 = 3
|
Ex. 2 - Qual o valor de "x" na equação  ? ?
Estamos perguntando: "Qual o expoente x que devemos
elevar a base 5 para resultar 6 ?". Aplicando a "volta" da equivalência
fundamental podemos escrever esta igualdade como sendo:

Este é o valor de x |
Ex. 2 (UFRGS) A forma exponencial da igualdade 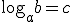 é: é:
(A) 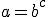
(B) 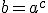
(C) 
(D) 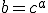
(E) 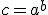
Esta é só aplicar a equivalência fundamental.
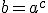
Resposta correta, letra "B". |
Veja agora alguns exemplos de aplicação da equivalência fundamental:
 |
Este é o
logaritmo que queremos saber. Primeiro de tudo devemos igualar a "x". |
 |
Agora é só
usar a equivalência fundamental |
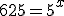 |
Caímos em
uma equação exponencial. Vamos fatorar! |
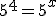
|
Bases igualada é só cortar. |
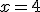
|
Esta é a resposta: 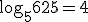 |
Mais um exemplo:
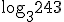
|
Sempre, o que devemos fazer primeiro é
igualar a "x". |
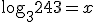
|
Aplicando a equivalência fundamental. |
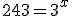
|
Esta é uma exponencial. Fatorando. |
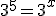
|
Cortando as bases |
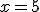
|
Esta é a resposta: 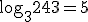 |
Mais um exemplo nunca é demais:
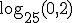
|
Igualando a "x". |

|
Aplicando a equivalência fundamental. |
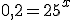
|
Agora para facilitar o cálculo, vamos
transformar o número decimal em fração e fatorar o que der. |

|
Aplicando as propriedades de potenciação. |
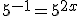
|
Cortando as bases. |
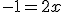

|
Esta é a resposta:  |
Esta é a técnica para se calcular o valor
do logaritmo de algum número em uma base definida. Na próxima página há alguns
exercícios para você resolver e comparar com a nossa resolução.
Veja no próximo
tópico as propriedades fundamentais de logaritmo para cálculo de equações.
|
