Página 1 de 1
(Ompara) Trigonometria
Enviado: 28 Mai 2021, 11:55
por Deleted User 23699
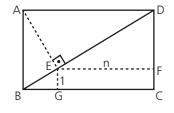
Na figura, o comprimento da diagonal BD no retângulo ABCD é d e E é o pé da perpendicular de BD em relação à A. Se a distância de E à reta BC é igual a 1 e a distância de E à reta CD é igual a n, então o valor da expressão
[tex3]2(d^{2/3}-n^{2/3})[/tex3]
é igual a
a) 1
b) 2
d) 3
d) 4
e) 5
- 61.png (4.32 KiB) Exibido 1034 vezes
Re: (Ompara) Trigonometria
Enviado: 26 Out 2023, 21:11
por παθμ
Seja [tex3]\theta=\angle EBG = \angle EAB = \angle EDA.[/tex3]
Seja também [tex3]x=BE, \; y=BG, \; a=AB, \; b=AD.[/tex3]
No triângulo BEG: [tex3]x=\frac{1}{\sin(\theta)},[/tex3]
[tex3]y=\frac{1}{\tan(\theta)}.[/tex3]
No triângulo ABE: [tex3]\sin(\theta)=\frac{x}{a} \Longrightarrow a=\frac{1}{\sin^2(\theta)}.[/tex3]
Também temos [tex3]a=d \sin(\theta) \Longrightarrow d=\frac{1}{\sin^3(\theta)}.[/tex3]
[tex3]DF=a-1=\frac{1}{\sin^2(\theta)}-1=\frac{1}{\tan^2(\theta)}.[/tex3]
Pitágoras no triângulo EFD: [tex3]n^2+\frac{1}{\tan^4(\theta)}=(d-x)^2=\left(d-\frac{1}{\sin(\theta)}\right)^2.[/tex3]
(Eq. 1)
[tex3]\sin(\theta)=\frac{1}{d^{1/3}} \Longrightarrow \tan^4(\theta)=\frac{1}{(d^{2/3}-1)^2}.[/tex3]
Plugando isso na Eq. 1: [tex3]n^2+(d^{2/3}-1)^2=(d-d^{1/3})^2 \Longrightarrow n^2=d^2-3d^{4/3}+3d^{2/3}-1=(d^{2/3}-1)^3 \Longrightarrow n^{2/3}=d^{2/3}-1 \Longrightarrow \boxed{2(d^{2/3}-n^{2/3})=2}[/tex3]
Alternativa B