Página 1 de 1
Eletrostática
Enviado: 22 Fev 2018, 16:34
por almeida13
Duas esferas condutoras iguais, de massa m e carga q, estão penduradas por um fio de seda de comprimento L, como na figura.Na posição inicial de equilíbrio, a distância entre as partículas vale X0. A seguir, descarregamos uma das esferas e nova “perfeição” de equilíbrio será X1, novamente, descarregamos uma das esferas e, no equilíbrio, a nova distância entre as esferas será X2. Após realizarmos N operações de descarga de uma das esferas, quanto valerá a distância Xn entre as partículas no equilíbrio, em função de L, K, q, m, g e N?
Considere o α pequeno, ou seja, sen α = tg α
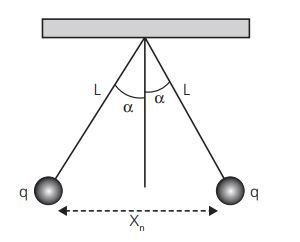
- xn.JPG (6.25 KiB) Exibido 2790 vezes
PS: Minha principal dúvida foi calcular a carga na enésima descarga.
Re: Eletrostática
Enviado: 22 Fev 2018, 21:35
por LucasPinafi
Minha interpretação foi a seguinte.
Depois que descarrega uma das esferas, a outra se aproxima, elas entram em contato e ocorre eletrização por contato. A informação que as esferas são iguais é exatamente para isso.. [tex3]Q_n = Q_{n-1}/2[/tex3]
Q1 => Q0/2
Q2 => Q1/2 = Q0/4
Q3 = Q2/2 = Q0/8
...
[tex3]Q_n = \frac{q}{2^n{}}[/tex3]
[tex3]T \cos \alpha = mg \\ T \sen \alpha = \frac{kq_n^2}{(2L \sen \alpha)^2} \\ \frac{T\sen \alpha}{T\cos \alpha} = \frac{kq^2_n}{4L^2mg \sen^2 \alpha } \\ \tg \alpha = \frac{kq_0^2}{4L^2 2^{2n}mg \sen^2 \alpha}\\ \tg^3 \alpha = \frac{kq_0^2}{4L^2 2^{2n} mg}\\
\tg \alpha = \sqrt[3]{\frac{kq_0^2}{4L^2 2^{2n} mg}} \\ X_n = 2L \tan \alpha = \sqrt[3] {\frac{2L kq_0^2}{L^2 2^{2n} mg}} = \sqrt[3]
{\frac{Lkq_0^2}{ 2^{2n-1} mg}}[/tex3]
é, bateu com o gabarito =D
Re: Eletrostática
Enviado: 22 Fev 2018, 21:40
por Andre13000
Ora, a carga da cada uma é q no começo. Depois q/2. Depois q/4. Temos:
[tex3]q=\frac{q_0}{2^n}[/tex3]
Temos que a retração entre as cargas é incialmente
[tex3]F=\frac{kq^2_0}{x_0^2}[/tex3]
Depois é de
[tex3]F=\frac{kq^2}{x^2}[/tex3]
Observe que pode-se considerar a força da gravidade [tex3]mg\sen\theta\approx mg\theta[/tex3]
. Temos
[tex3]2\theta_nL=x_n\to \theta=\frac{x_n}{2L}[/tex3]
Para entender expressão acima, considere um pequeno arco de raio L e ângulo teta. Seu comprimento é dado pelo produto dessas grandezas.
Portanto
[tex3]mg\sen \theta_n=\frac{mg x_n}{2L}=\frac{kq^2}{x_n^2}\\
x_n^3=\frac{kLq^2_0}{2^{2n-1}mg}[/tex3]
A resposta segue de imediato.
Re: Eletrostática
Enviado: 08 Dez 2022, 12:09
por TenBatistta
Olá!
A partir de que vocês afirmaram que a carga inical vai para Q/4, Q/8... ?
Re: Eletrostática
Enviado: 08 Mar 2024, 09:44
por gouy
LucasPinafi escreveu: ↑22 Fev 2018, 21:35
[tex3]
\tg \alpha = \frac{kq_0^2}{4L^2 2^{2n}mg \sen^2 \alpha}\\ \tg^3 \alpha = \frac{kq_0^2}{4L^2 2^{2n} mg}\\
\tg \alpha = \sqrt[3]{\frac{kq_0^2}{4L^2 2^{2n} mg}} \\[/tex3]
Como [tex3]tg\alpha [/tex3]
virou [tex3]tg\alpha ^{3}[/tex3]
sendo que no denominador só tinha [tex3]sen^{2}\alpha [/tex3]
?? Faltava o [tex3]cos^{2}\alpha [/tex3]
.
Re: Eletrostática
Enviado: 15 Mar 2024, 20:38
por LucasPinafi
gouy escreveu: ↑08 Mar 2024, 09:44
LucasPinafi escreveu: ↑22 Fev 2018, 21:35
[tex3]
\tg \alpha = \frac{kq_0^2}{4L^2 2^{2n}mg \sen^2 \alpha}\\ \tg^3 \alpha = \frac{kq_0^2}{4L^2 2^{2n} mg}\\
\tg \alpha = \sqrt[3]{\frac{kq_0^2}{4L^2 2^{2n} mg}} \\[/tex3]
Como [tex3]tg\alpha [/tex3]
virou [tex3]tg\alpha ^{3}[/tex3]
sendo que no denominador só tinha [tex3]sen^{2}\alpha [/tex3]
?? Faltava o [tex3]cos^{2}\alpha [/tex3]
.
Veja o enunciado. Ele fala [tex3]\sin \alpha \approx \tan \alpha[/tex3]
. Nessa situação, [tex3]\cos \alpha \approx 1[/tex3]
.