Estude! Com Prof. Caju

Existe algum número da forma qqpp que seja quadrado perfeito, onde p e q são algarismos e q [tex3]\neq[/tex3] 0?

Pelo critério de divisibilidade esse número é divisível por 11.

Mas: $11^{4} = 14641 > qqpp$

Então:

$qqpp = 11^2 \cdot 2^a \cdot 3^b \cdot ....$

Usando base 10:

$1000q + 100q + 10p + p =$
$1100q + 11p =$
$11\cdot (100q + p) =$

Devemos ter:

$100q + p \equiv 0 \mod(11)$

Como p e q são algarismos e $q \neq 0$ , vejamos:

$100q + p = 11k^2$
$q = \frac{11k^2 - p }{100}$

Assim:

$1 \leq \frac{11k^2 - p }{100} \leq 9$
$100 \leq 11k^2 - p \leq 900$

Como p é apenas um algarismo, ou seja, varia entre 0 e 9, então:

$4 \leq k \leq 9$

Dá pra testar de boa:

Para k = 4
$q = \frac{11\cdot 4^2 - p }{100} = \frac{176 - p }{100}$
Para k = 5
$q = \frac{11\cdot 5^2 - p }{100} = \frac{275 - p }{100}$
Para k = 6
$q = \frac{11\cdot 6^2 - p }{100} = \frac{396 - p }{100}$
Para k = 7
$q = \frac{11\cdot 7^2 - p }{100} = \frac{539 - p }{100}$
Para k = 8
$q = \frac{11\cdot 8^2 - p }{100} = \frac{704 - p }{100}$
Para k = 9
$q = \frac{11\cdot 8^2 - p }{100} = \frac{891 - p }{100}$

O único caso promissor é se $k = 8$ , porque daí teríamos:
$p = 4$
$q = 7$

Testando:

$qqpp = 7744$

Assim:

$\sqrt{7744} = 88$

Achamos

Um número "qqpp" pode ser escrito algebricamente como $1000q+100q+10p+p$ . Queremos que isto seja um quadrado perfeito, então:
$1100q+11p=x^2 \rightarrow 11(100q+p)=x^2$
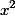
Da relação acima, tiramos que $x^2$ é um múltiplo de 11, mas como trata-se de um quadrado perfeito, esse fator 11 não pode apenas uma vez sozinho no x, então temos necessariamente que $x^2=(11t)^2$
$11(100q+p)=(11t)^2 \rightarrow 100q+p=11t^2$
Temos então que "q0p" = $11t^2$ . Dessa vez, "q0p" precisa ser divisível por 11. O critério de divisibilidade por 11 nos diz que a soma dos algarimos ímpares menos a soma dos algarísmos pares deve ser divisível por 11 para que o número seja divísivel por 11. Assim:
$(p+q)-(0)=11k \rightarrow p+q=11k$
Como p e q são algarismos, ou seja, estão entre 0 e 9, e não queremos q=0, temos necessariamente que $p+q=11$
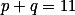
De solução para esta equação, temos os seguintes pares: $(2,9);(3,8);(4,7);(5,6);(6,5);(7,4);(8,3);(9,2)$ , resultando nos números 209, 308, 407, 506, 605, 704, 803 e 902, respectivamente. Escrevendo esses números como 11 vezes alguma coisa, obtemos 11.19, 11.28, 11.37, 11.46, 11.55, 11.64, 11.73 e 11.82, respectivamente. Desses, o único da forma $11t^2$ é o 11.64, ou seja, $t=8$
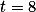
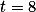
Com $t=8$ , obtemos $x^2=(11*8)^2=7744$
Então existe apenas um número do tipo qqpp, tal que $q\neq0$ , que é um quadrado perfeito, o 7744.
Creio que seja esta a resolução.

EDIT: O Ittalo25 postou sua resolução antes de mim, mas vou deixá-la aqui de qualquer forma.

Estude! Com Prof. Caju

(XXII-OPM) Quadrados Perfeitos

(XXII-OPM) Quadrados Perfeitos

Re: (XXII-OPM) Quadrados Perfeitos

Re: (XXII-OPM) Quadrados Perfeitos