Página 1 de 1
(ESPCEX - 1996) Função
Enviado: 21 Mai 2012, 09:52
por gabrielifce
Um fio de comprimento L é cortado em dois pedaços um dos quais formará um quadrado e o outro um triângulo equilátero. Para que a soma das áreas do quadrado e do triângulo seja mínima, o fio deve ser cortado de forma que o comprimento do lado do triângulo seja:
[tex3]a) \frac{3L}{7}\\
b) \frac{L(9-4\sqrt{3})}{11}\\
c) \frac{\sqrt{3}L}{9+4\sqrt{3}}\\
D) \frac{3L}{2}\\
E) \frac{\sqrt{3}L}{3}[/tex3]
Re: (ESPCEX - 1996) Função
Enviado: 21 Mai 2012, 11:56
por emanuel9393
Olá, gabrielifce!
Eu fiz o seguinte:
O fio foi dividido em duas partes:
e
. Vamos considerar que o pedaço de comprimento
tenha sido usado para formar o triângulo equilátero:
Área do triângulo:
^{2} \sqrt{3}}{2} \, = \, \frac{\frac{x^{2}}{9} \sqrt{3}}{2} \, = \, \boxed{\frac{x^{2} \sqrt{3}}{18}} "A_{t} \, = \, \frac{\left(\frac{x}{3}\right)^{2} \sqrt{3}}{2} \, = \, \frac{\frac{x^{2}}{9} \sqrt{3}}{2} \, = \, \boxed{\frac{x^{2} \sqrt{3}}{18}}")
Área do quadrado:
^{2} \, = \, \boxed{\frac{L^{2} \, - \,2Lx \, + \,x^{2}}{4}} "A_{q}\, = \, \left(\frac{L \, - \, x}{4}\right)^{2} \, = \, \boxed{\frac{L^{2} \, - \,2Lx \, + \,x^{2}}{4}}")
Logo:
L \, + \, \left(\frac{1}{4} \, + \, \frac{\sqrt{3}}{18}\right)x^{2} "A_{total} \, = \, A_{q} \, + \, A_{t} \\ A_{total} \, = \, \frac{L^{2} \, - \,2Lx \, + \,x^{2}}{4} \, + \, \frac{x^{2} \sqrt{3}}{18} \\ \\ A_{total} \, = \, \frac{1}{4}L^{2} \, - \, \left(\frac{1}{2}x\right)L \, + \, \left(\frac{1}{4} \, + \, \frac{\sqrt{3}}{18}\right)x^{2}")
Só que essa equação apresenta somente valor máximo. Sinceramente, não sei o que há de errado.
Um abraço!
Re: (ESPCEX - 1996) Função
Enviado: 21 Mai 2012, 11:56
por VALDECIRTOZZI
Digamos que cortamos a uma distância
da borda do fio.
Então
será o lado do triâgulo equilátero e
será o lado do quadrado.
Sendo
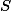
a soma das áreas:
^2\sqrt3}{4}+\left(\frac{L-x}{4}\right)^2 "S=\frac{(\frac{x}{3})^2\sqrt3}{4}+\left(\frac{L-x}{4}\right)^2")
}{144} "S=\frac{x^2\sqrt3}{36}+\frac{L^2-2Lx+x^2}{16}=\frac{4x^2\sqrt3+9(L^2-2Lx+x^2)}{144}")
-18Lx+9L^2}{144} "S=\frac{4x^2\sqrt3+9L^2-18Lx+9x^2}{144}=\frac{x^2(4\sqrt3+9)-18Lx+9L^2}{144}")
Para que a soma das áreas seja mínima, temos que
}=\frac{9L}{4\sqrt3+9}=\frac{9L(4\sqrt3-9)}{(4\sqrt3+9)(4\sqrt3-9)}=\frac{36L\sqrt3-81L}{48-81}=\frac{36L\sqrt3-81L}{(-33)}=\frac{9L(4\sqrt3-9)}{(-33)}=\frac{3L(9-4\sqrt3)}{11} "x=-\frac{\frac{-18L}{144}}{2 \cdot (\frac{4\sqrt3+9}{144})}=\frac{9L}{4\sqrt3+9}=\frac{9L(4\sqrt3-9)}{(4\sqrt3+9)(4\sqrt3-9)}=\frac{36L\sqrt3-81L}{48-81}=\frac{36L\sqrt3-81L}{(-33)}=\frac{9L(4\sqrt3-9)}{(-33)}=\frac{3L(9-4\sqrt3)}{11}")
O lado do triângulo é
}{11\cdot 3}=\frac{L(9-\sqrt3)}{11} "\frac{x}{3}=\frac{3L(9-4\sqrt3)}{11\cdot 3}=\frac{L(9-\sqrt3)}{11}")
Espeor ter ajudado.
Re: (ESPCEX - 1996) Função
Enviado: 02 Mai 2015, 14:54
por brunoafa
Muito foda essa questão, quem diria que é da EsPCEx!
Re: (ESPCEX - 1996) Função
Enviado: 02 Mai 2015, 14:58
por brunoafa
VALDECIRTOZZI escreveu:
Para que a soma das áreas seja mínima, temos que
Por que
e não
??
Re: (ESPCEX - 1996) Função
Enviado: 02 Mai 2015, 15:26
por emanuel9393
Olá, brunoafa!
Não se esqueça das expressões que definem as coordenadas do vértice:
O seja,
corresponde à ordenada do vértice e não a abcissa.
Grande abraço!
Re: (ESPCEX - 1996) Função
Enviado: 02 Mai 2015, 15:47
por brunoafa
emanuel9393 escreveu:Olá, brunoafa!
Não se esqueça das expressões que definem as coordenadas do vértice:
O seja,
corresponde à ordenada do vértice e não a abcissa.
Grande abraço!
Sim, eu sei, mas como a>0 a função admite valor mínimo
- url.gif (3.13 KiB) Exibido 2994 vezes
Por que pegar o x do vértice e não o y?
Acho que estou confundindo com a física que tem problemas de distância mínima entre dois corpos, mas mesmo assim não entendi muito bem isso.
Re: (ESPCEX - 1996) Função
Enviado: 02 Mai 2015, 23:28
por emanuel9393
Olá, brunoafa!
Procure entender. Nesse caso, a soma das áreas
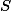
é uma função do segundo grau em
. Em outras palavras, em um gráfico de
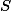
em função de
, o
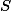
é a ordenada e o
é a abcissa. O que ele fez foi procurar o valor de
que produz o
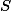
mínimo. Nesse caso, determinar o
para o
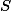
mínimo permite determinar o lado do triângulo que é o que o problema pede. Entendeu?
Grande abraço!