Página 1 de 1
Triângulo
Enviado: 25 Abr 2024, 13:55
por botelho
Se U incentro do triângulo DAR e I incentro do triângulo ARO, DR//UN e o valo da razão aritmética entre os inradios dos triângulos DRO e UNI é 4.Calcular UI.
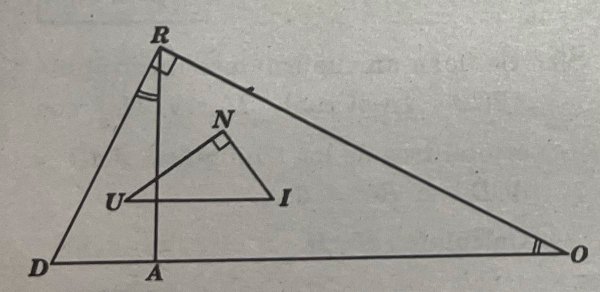
- IMG-20240424-WA0021.jpg (26.7 KiB) Exibido 170 vezes
a)8
b)7
c)6
d)5
e)4
Re: Triângulo
Enviado: 30 Abr 2024, 10:05
por petras
botelho,
O raio do triângulo DRO(CH) é igual a IN = NU e portanto o triângulo UNI seria um retângulo isósceles.
Demonstração:
Se: DA=a, AR=b:
[tex3]\triangle DRO: b^2 = a.AO \implies AO=\frac{b^2}{a}\\
\triangle DRA: DR^2=a^2+b^2 \implies DR=\sqrt{a^2+b^2}\\
\triangle DRO: OR^2 = AO.DO = \frac{b^2}{a}.(a+\frac{b^2}{a}) = \frac{b^2}{a^2}(a^2+b^2) \\
OR=\frac{b}{a}(\sqrt{a^2+b^2})[/tex3]
.
Se r, R e x são os inraios dos triângulos DAR, OAR e DRO respectivamente: (inraio é a relação entre o dobro da área e o perímetro: [tex3]S = p.r = \frac{2pr}{2} \therefore 2S = 2p.r[/tex3]
)
[tex3]r=\frac{ab}{a+b+\sqrt{a^2+b^2}}\\
R=\frac{b^2}{a+b+\sqrt{a^2+b^2}}\\
x=\frac{b\sqrt{a^2+b^2}}{a+b+\sqrt{a^2+b^2}}[/tex3]
Por outro lado, teremos triángulos semelhantes:
[tex3]UN:r=\sqrt{a^2+b^2}: a \implies \boxed{UN=\frac{b\sqrt{a^2+b^2}}{a+b+\sqrt{a^2+b^2}}=x}\\
IN:R=\frac{b}{a}\sqrt{a^2+b^2}:(\frac{b^2}{a}) \implies :\boxed{IN=\frac{b\sqrt{a^2+b^2}}{a+b+\sqrt{a^2+b^2}}=x}
[/tex3]
x é o inraio do triángulo UNI:
[tex3]x′=\frac{x^2}{2x+\sqrt 2 x}=\frac{x}{2+\sqrt2}\\
x−x′=4 \implies x=4\sqrt 2
\therefore UI=x\sqrt 2= \boxed{8}[/tex3]
(Solução: Intelligentipauca-adaptada)