Página 1 de 1
O triângulo e a mediana
Enviado: 01 Jan 2023, 19:12
por fibonacci
Os segmentos congruentes [tex3]AE[/tex3]
e [tex3]AF[/tex3]
são tomados sobre os lados [tex3]AB[/tex3]
e [tex3][/tex3]
,
respectivamente, do triângulo [tex3]ABC[/tex3]
. A mediana [tex3]AM[/tex3]
intersecta [tex3]EF[/tex3]
em [tex3]Q[/tex3]
. Prove que
[tex3]\dfrac{QE}{QF}=\dfrac{AC}{AB}[/tex3]
.
Re: O triângulo e a mediana
Enviado: 02 Jan 2023, 15:46
por leozitz
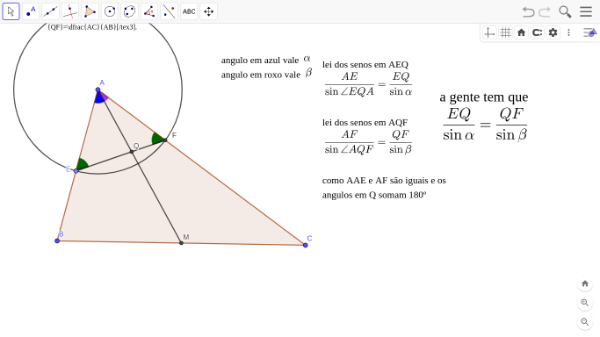
- olimp.png (47.14 KiB) Exibido 523 vezes
agora a gente faz algo semelhante para os triangulos ABM e ACM
[tex3]\frac{BM}{\sin\alpha} = \frac{AB}{\sin\angle AMB}\implies AB\cdot\sin\alpha = BM\sin\angle AMB[/tex3]
fazendo a mesma coisa para o triangulo ACM a gente conclui que
[tex3]AB\cdot \sin\alpha = BC\cdot \sin\beta\\
\frac{AB}{BC}=\frac{\sin\beta}{\sin\alpha}[/tex3]
manipulando [tex3]\frac{EQ}{\sin\alpha} = \frac{FQ}{\sin\beta}[/tex3]
e igualando a gente chega no resultado
a ideia dessa solução é achar um jeito de calcular os segmentos QF e QE com coisas em comum ao triangulo ABC, por exemplo, os angulos alpha e beta
que aparecem nos triangulos AQE e ABM e nos triangulos AQF e ACM
Re: O triângulo e a mediana
Enviado: 02 Jan 2023, 16:49
por petras
fibonacci,
[tex3]\mathsf{Unir~BF\\
BF\cap AD=P\\
T.Menelaus:\\
\triangle EBF_{AP}: \frac{AE}{AB}.\frac{BP}{FP}.\frac{FQ}{EQ} = 1\implies \boxed{\frac{FQ}{EQ}=\frac{AB}{AE}.\frac{FP}{BP}}(I)\\
\triangle FBC_{AD}: \frac{AF}{AC}.\frac{BP}{FP}.\frac{\cancel{CD}}{\cancel{BD}}=1\implies \boxed{\frac{AF}{AC}=\frac{FP}{BP}}(II)\\
(II)em(I): \frac{FQ}{EQ}=\frac{AB}{\cancel{AE}}.\frac{\cancel{AF}}{AC} =\frac{AB}{AC}\\
\therefore \boxed{\boxed{\frac{EQ}{FQ} =\frac{AC}{AB}}}c.q.d
}
[/tex3]