a imagem:
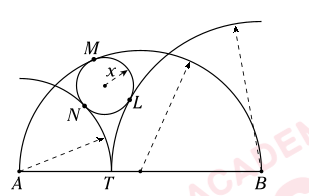
- a imagem.png (15.93 KiB) Exibido 2179 vezes
o problema do meio é o mais difícil e eu cheguei em uma expressão estranha.
Você pode sempre apelar para as cônicas:
Sejam:
[tex3]Z[/tex3]
ponto médio de [tex3]AB[/tex3]
[tex3]X = \odot (A,AT) \cap \odot(Z,ZA)[/tex3]
trace a elipse de focos [tex3]A,Z[/tex3]
passando por [tex3]X[/tex3]
trace a elipse de focos [tex3]B,Z[/tex3]
passando por [tex3]Y = \odot (B,BT) \cap \odot(Z,ZB)[/tex3]
o encontro dessas duas elipses é o centro do círculo procurado
a basta ligar este com o ponto Z e você tem o círculo.
Eu tentei fazer algebricamente essa brincadeira:
fixando [tex3]AB =2[/tex3]
e colocando a origem do plano complexo em [tex3]Z[/tex3]
.
O ponto [tex3]T[/tex3]
corresponde a um número real [tex3]-1<t<1[/tex3]
de forma que ele está sobre o segmento [tex3]AB[/tex3]
.
Porém ao resolver as expressões das elipses no plano complexo chegamos em uma cúbica.
Se o wolframalpha não me enganou o centro da circunferência é o ponto:
[tex3]z = \frac14(5t-t^3, (1-t^2)\sqrt{9-t^2})[/tex3]
https://www.wolframalpha.com/input/?i=% ... -1%3Ct%3C1
o que é meio estranho, mas parece verdade.
[tex3]|z| = \frac14 |(5t-t^3, (1-t^2)\sqrt{9-t^2})| = \frac{t^2+3}4[/tex3]
portanto o raio do círculo menor é [tex3]\frac{1-t^2}4[/tex3]
sempre, o que é bem simples.
Mas o wolfram não me deixa continuar a brincadeira e encontrar N e L:
https://www.wolframalpha.com/input/?i=% ... -1%3Ct%3C1