Ensino Médio

Mensagem não lidapor **ALDRIN** » 20 Abr 2009, 13:41 · Mensagem não lida por **ALDRIN** » 20 Abr 2009, 13:41

Duas circunferências de raios [tex3]R[/tex3] e [tex3]r[/tex3] cortam-se ortogonalmente. Traça-se a tangente externa [tex3]BC[/tex3] ( [tex3]B[/tex3] e [tex3]C[/tex3] pontos de contato). Calcular o raio da circunferência que é tangente externamente às duas primeiras e tangente a reta [tex3]BC[/tex3] .

Mensagem não lidapor **caju** » 29 Abr 2012, 12:28 · Mensagem não lida por **caju** » 29 Abr 2012, 12:28

Olá Aldrin,

Circunferências cortando-se em um determinado ângulo significa que no ponto de intersecção entre elas, as retas tangentes possuem aquele ângulo.
Ou seja, como neste exercício é dito que se cortam perpendicularmente, veja o ângulo $\angle O_1DO_2$ da figura abaixo:

Veja a figura da questão:

: Screen Shot 2012-04-29 at 12.00.46.png (38.99 KiB) Exibido 916 vezes

Vamos dizer que o raio do círculo de centro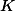 $K$ é $x$ .

Olhando para o triângulo $O_1DO_2$ e aplicando Pitágoras:

$R^2+r^2=(\overline{O_1O_2})^2$

$\boxed{\overline{O_1O_2}=\sqrt{R^2+r^2}}$

Agora olhamos para o triângulo $O_1AO_2$ e aplicamos pitágoras:

$(\overline{AO_1})^2+(\overline{AO_2})^2=(\overline{O_1O_2})^2$

$(R-r)^2+(\overline{AO_2})^2=(\sqrt{R^2+r^2})^2$

$\boxed{\overline{AO_2}=\sqrt{2Rr}}\text{ (I)}$

Guardamos esta equação e vamos pensar no triângulo $LO_1K$ e aplicar Pitágoras:

$(\overline{LO_1})^2+(\overline{LK})^2=(\overline{KO_1})^2$

$(R-x)^2+(\overline{LK})^2=(R+x)^2$

$\boxed{\overline{LK}=2\sqrt{Rx}}\text{ (II)}$

Pensando agora no triângulo $KMO_2$ e aplicando pitágoras:

$(\overline{MO_2})^2+(\overline{MK})^2=(\overline{KO_2})^2$

$(r-x)^2+(\overline{MK})^2=(r+x)^2$

$\boxed{\overline{MK}=2\sqrt{rx}}\text{ (III)}$

É fácil ver que $\overline{AO_2}=\overline{LM}$ e que, portanto, $\boxed{\overline{AO_2}=\overline{LK}+\overline{MK}}\text{ (IV)}$

Substituindo (I), (II) e (III) em (IV), temos:

$\sqrt{2Rr}=2\sqrt{Rx}+2\sqrt{rx}$

Colocando o $2\sqrt{x}$ em evidência do lado direito da igualdade:

$\sqrt{2Rr}=2\sqrt{x}\cdot(\sqrt{R}+\sqrt{r})$

$\sqrt{x}=\frac{\sqrt{2Rr}}{2\cdot(\sqrt{R}+\sqrt{r})}$

Elevando ambos os lados ao quadrado:

$\boxed{\boxed{x=\frac{Rr}{2\cdot(R+r+2\sqrt{Rr})}}}$

Grande abraço,
Prof. Caju

Ensino Médio ⇒ Geometria

Geometria

Re: Geometria

Ensino Médio ⇒ Geometria

Geometria

Re: Geometria

Entrar | Registrar