Olimpíadas

cicero444 · Mensagem não lida por **cicero444** » 06 Jul 2015, 09:43

Um inteiro positivo n é chamado perfeito se a soma de todos os seus divisores excluindo n, é igual a n. Prove que um número perfeito maior do que 28 é divisível por 7 então ele é divisível por 49.

Mensagem não lidapor **Ittalo25** » 06 Jul 2015, 16:39 · Mensagem não lida por **Ittalo25** » 06 Jul 2015, 16:39

Pensei nisto:

Do enunciado:

$(\frac{{7}^{x+1}-1}{7-1})\cdot (\frac{p_2^{k_2+1} - 1}{p_2 - 1}) \cdot \cdot \cdot (\frac{p_j^{k_j+1}-1}{p_j - 1}) = 2n$

$(\frac{p_2^{k_2+1} - 1}{p_2 - 1}) \cdot \cdot \cdot (\frac{p_j^{k_j+1}-1}{p_j - 1}) = \frac{12n}{{7}^{x+1}-1}$

Isso deve ser inteiro porque é a soma dos divisores de $\frac{n}{7^x}$ que é inteiro.

$12n\geq }{{7}^{x+1}-1}> 12.28$

${7}^{x+1}> 337$

${7}^{x+1}> 337$

${7}^{x+1}\geq 7^3 > 337$

$x+1}\geq 3$

$x\geq 2$

suponha
$n = 7*p_2^{x_1}*...*p_k^{x_{k-1}} > 28$
$\frac n7 = p_2^{x_1}*...*p_k^{x_{k-1}} > 4$
então
$2n = \frac{48}{6}\frac{(p_2^{x_1+1}-1)...(p_k^{x_{k-1}+1}-1)}{(p_2-1)...(p_k-1)}$
$n = 4\frac{(p_2^{x_1+1}-1)...(p_k^{x_{k-1}+1}-1)}{(p_2-1)...(p_k-1)}$
logo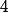 $4$ divide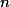 $n$

$7*p_2^{x_1}*...*p_k^{x_{k-1}} = 4*\frac{(p_2^{x_1+1}-1)...(p_k^{x_{k-1}+1}-1)}{(p_2-1)...(p_k-1)}$
$7*(p_2^{x_1+1}-p_2^{x_1})*...*(p_k^{x_{k-1}+1}-p_k^{x_{k-1}}) = 4*(p_2^{x_1+1}-1)...(p_k^{x_{k-1}+1}-1)$

de onde existe um $p_i$ com $p_i^{x_i+1} \equiv 1 \mod 7$ $x_i \geq 1, x_i+1\geq 2$
$x_i+1 = k*ord_7 p_i$
$ord_7 p_i \in \{1,2,3,6\}$

a idéia é provar que algum p também é 7 ou que não pode ter só um 7 e todos os outros primos diferentes de 7

Olimpíadas ⇒ (Rússia-2000) Teoria dos Números

(Rússia-2000) Teoria dos Números

Re: (Rússia-2000) Teoria dos Números

Re: (Rússia-2000) Teoria dos Números

Olimpíadas ⇒ (Rússia-2000) Teoria dos Números

(Rússia-2000) Teoria dos Números

Re: (Rússia-2000) Teoria dos Números

Re: (Rússia-2000) Teoria dos Números

Entrar | Registrar