Ensino Superior ⇒ Geometria Analítica - Retas e Planos Tópico resolvido
- ilprofeta

- Mensagens: 12
- Registrado em: 19 Jun 2014, 22:22
- Última visita: 25-08-22
- Agradeceu: 10 vezes
- Agradeceram: 5 vezes
Jun 2014
30
11:54
Geometria Analítica - Retas e Planos
Dados os pontos ) ,
, ) ,
, ) e
e ) , sejam
, sejam  ,
,  e
e 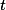 as retas que contêm os segmentos
as retas que contêm os segmentos  ,
,  e
e  , respectivamente. Encontre uma equação geral do plano
, respectivamente. Encontre uma equação geral do plano 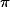 paralelo ao plano que passa pelos pontos
paralelo ao plano que passa pelos pontos 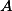 ,
, 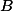 ,
, 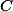 e de modo que a área do triângulo ABC seja igual a
e de modo que a área do triângulo ABC seja igual a  , onde
, onde 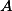 ,
, 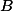 e
e 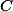 são os pontos de intersecção das retas
são os pontos de intersecção das retas  ,
,  e
e 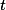 com o plano
com o plano 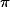 , respectivamente.
, respectivamente.
Editado pela última vez por ilprofeta em 30 Jun 2014, 11:54, em um total de 1 vez.
- Juniorhw

- Mensagens: 634
- Registrado em: 14 Jan 2013, 17:10
- Última visita: 19-08-20
- Agradeceu: 93 vezes
- Agradeceram: 458 vezes
Jul 2014
02
23:13
Re: Geometria Analítica - Retas e Planos
Vou fazer da maneira mais geral. Vamos primeiro achar o plano que passa pelos três pontos dados. O vetor normal do plano pode ser dado pelo produto vetorial de dois vetores não colineares contidos nesse plano. Pegando os vetores ) e
e ) e calculando o produto vetorial:
e calculando o produto vetorial:
)
Logo o plano pode ser descrito por:
+3y+2z=0\\\\\Rightarrow 6x+3y+2z-6=0)
Um plano paralelo a esse tem equação da forma
As retas ,
,  e
e 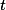 são os próprios eixos, logo, achando as intersecções:
são os próprios eixos, logo, achando as intersecções:
)
)
)
A área do triângulo é metade do módulo do produto vetorial
é metade do módulo do produto vetorial  :
:
)
O módulo é:

A metade disso é a área de , que foi dada, logo:
, que foi dada, logo:

e as possíveis equações do plano são:

Creio que seja isso,
Abraço.
Logo o plano pode ser descrito por:
Um plano paralelo a esse tem equação da forma
As retas
A área do triângulo
O módulo é:
A metade disso é a área de
e as possíveis equações do plano são:
Creio que seja isso,
Abraço.
Editado pela última vez por Juniorhw em 02 Jul 2014, 23:13, em um total de 1 vez.
-
- Tópicos Semelhantes
- Resp.
- Exibições
- Últ. msg
-
- 2 Resp.
- 904 Exibições
-
Últ. msg por monicarneiro
-
- 2 Resp.
- 1105 Exibições
-
Últ. msg por monicarneiro
-
- 1 Resp.
- 674 Exibições
-
Últ. msg por edinaely84
-
- 0 Resp.
- 616 Exibições
-
Últ. msg por luckbrav
-
- 1 Resp.
- 1852 Exibições
-
Últ. msg por csmarcelo
