Encontre todos os primos [tex3]p[/tex3]
, para os quais o quociente.
[tex3]\frac{2^{p-1}-1}{p}[/tex3]
é um quadrado perfeito.
Olá, Comunidade!
Vocês devem ter notado que o site ficou um período fora do ar (do dia 26 até o dia 30 de maio de 2024).
Consegui recuperar tudo, e ainda fiz um UPGRADE no servidor! Agora estamos em um servidor dedicado no BRASIL!
Isso vai fazer com que o acesso fique mais rápido (espero )
)
Já arrumei os principais bugs que aparecem em uma atualização!
Mas, se você encontrar alguma coisa diferente, que não funciona direito, me envie uma MP avisando que eu arranjo um tempo pra arrumar!
Vamos crescer essa comunidade juntos
Grande abraço a todos,
Prof. Caju
Vocês devem ter notado que o site ficou um período fora do ar (do dia 26 até o dia 30 de maio de 2024).
Consegui recuperar tudo, e ainda fiz um UPGRADE no servidor! Agora estamos em um servidor dedicado no BRASIL!
Isso vai fazer com que o acesso fique mais rápido (espero
Já arrumei os principais bugs que aparecem em uma atualização!
Mas, se você encontrar alguma coisa diferente, que não funciona direito, me envie uma MP avisando que eu arranjo um tempo pra arrumar!
Vamos crescer essa comunidade juntos
Grande abraço a todos,
Prof. Caju
Olimpíadas ⇒ Números primos
Moderador: [ Moderadores TTB ]
-
Auto Excluído (ID:12031)

- Última visita: 31-12-69
Jun 2014
19
22:36
Re: Números primos
Cara, não consegui resolver ainda mas vou deixar aqui algumas observações que eu acho que podem ajudar a resolver esse problema:
Se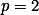 teremos:
teremos:
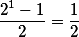
então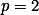 não nos convém.
não nos convém.
Pelo pequeno teorema de fermat se=1) e
e 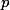 é primo então:
é primo então:
)
Se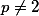 então o pequeno teorema de fermat garante que
então o pequeno teorema de fermat garante que
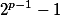 é múltiplo de
é múltiplo de 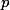
o problema pede que:
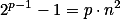
como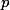 é ímpar podemos dizer que
é ímpar podemos dizer que 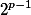 é um quadrado perfeito. Pois o expoente é par. Mais do que isso
é um quadrado perfeito. Pois o expoente é par. Mais do que isso 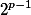 não é divisível por 3. Pois é uma potência de 2.
não é divisível por 3. Pois é uma potência de 2.
Lema: Todo quadrado perfeito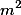 quando dividido por 3 deixa restos:
quando dividido por 3 deixa restos:
1 - se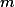 não for múltiplo de 3
não for múltiplo de 3
0 - se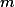 é múltiplo de 3
é múltiplo de 3
Prova: ou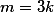 pra
pra 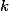 inteiro positivo então
inteiro positivo então )
ou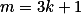 então
então +1)
ou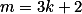 então
então +1)
cqd
então temos que \rightarrow 2^{p-1} - 1 \equiv 0\, mod(3)) então devemos ter que:
então devemos ter que:
)
excetuando-se o caso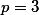 que satisfaz a condição do problema pois:
que satisfaz a condição do problema pois:
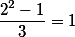
devemos ter então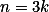 e é fácil ver que
e é fácil ver que 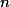 deve ser ímpar, pois
deve ser ímpar, pois 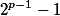 é ímpar e
é ímpar e 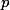 também é. Então
também é. Então ) .
.
Com esta descoberta podemos inferir agora que se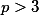 então
então )
observemos que:
)
)
)
)
\equiv 16\, mod(9) \equiv 7\, mod(9))
\equiv 5 \, mod(9))
\equiv 10\,mod(9) \equiv 1\,mod(9))
e a partir dai o padrão se repete.
Então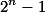 só é divisível por 9 se
só é divisível por 9 se 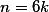 pra algum
pra algum 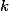 inteiro não-negativo, então temos que
inteiro não-negativo, então temos que )
teremos:
^2)
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 4. Todo quadrado perfeito par é divisível por 4.
Prova: Seja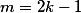 então
então +1)
pra os primos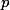 com
com 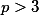 temos que
temos que 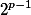 é divisível por 4 então:
é divisível por 4 então:
)
do lado direito:
^2 \equiv p\,mod(4))
então
 \rightarrow p =4x +3(**))
) e
e ) :
: 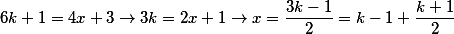

vou só mostrar que deve ser ímpar e deixar indicada a PA em que
deve ser ímpar e deixar indicada a PA em que 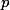 se encontra. Pelo teorema de Dirichlet para progressões aritméticas, temos que existem infinitos primos nessa sequência, então eu não resolvi o problema, mas o restringi um pouco. Espero que isso sirva pra alguém.
se encontra. Pelo teorema de Dirichlet para progressões aritméticas, temos que existem infinitos primos nessa sequência, então eu não resolvi o problema, mas o restringi um pouco. Espero que isso sirva pra alguém.
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 8.
Prova: Seja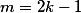 então
então +1)
é fácil ver que) é par.
é par.
pra os primos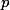 com
com 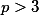 temos que
temos que 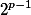 é divisível por 8 então:
é divisível por 8 então:
)
do lado direito:
^2 \equiv p\,mod(8))
então
 \rightarrow p =8z +7 = 4x + 3\rightarrow x=2z+1) cqd
cqd
como
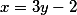 então
então 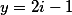
-2)+3 =4(6i-5)+3=24i-17)
alguns candidatos a solução são: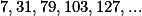
Se
então
Pelo pequeno teorema de fermat se
Se
o problema pede que:
como
Lema: Todo quadrado perfeito
1 - se
0 - se
Prova: ou
ou
ou
cqd
então temos que
excetuando-se o caso
devemos ter então
Com esta descoberta podemos inferir agora que se
observemos que:
e a partir dai o padrão se repete.
Então
teremos:
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 4. Todo quadrado perfeito par é divisível por 4.
Prova: Seja
pra os primos
do lado direito:
então
vou só mostrar que
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 8.
Prova: Seja
é fácil ver que
pra os primos
do lado direito:
então
como
alguns candidatos a solução são:
Editado pela última vez por Auto Excluído (ID:12031) em 19 Jun 2014, 22:36, em um total de 1 vez.
-
Auto Excluído (ID:12031)

- Última visita: 31-12-69
Jan 2015
09
11:11
Re: Números primos
logo para todo primo da forma
excetuando-se o caso
Editado pela última vez por Auto Excluído (ID:12031) em 09 Jan 2015, 11:11, em um total de 1 vez.
-
Vinisth

- Mensagens: 1244
- Registrado em: 10 Jun 2010, 23:39
- Última visita: 11-07-23
- Agradeceu: 44 vezes
- Agradeceram: 903 vezes
Jan 2015
09
11:58
Re: Números primos
Ol,á a todos,
Primeiro faz-se o teste com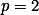 , como sousóeu fez.
, como sousóeu fez.
Todo primo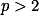 é ímpar, logo seja p da foma
é ímpar, logo seja p da foma (2^n+1)=(2n+1)x^2)
Como=1) e cada fator é um número ímpar consecutivo, a equação se torna em resolver :
e cada fator é um número ímpar consecutivo, a equação se torna em resolver :

(t+1))
Ambos fatores devem ser potências de 2, isso só acontece
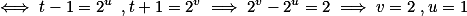
Logo, só tem solução para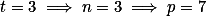 , analogamente pode-se ter
, analogamente pode-se ter 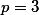 .
.
Os números são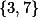
Para complemento: Fermat Quotient
Abraço !
Primeiro faz-se o teste com
Todo primo
Como
Ambos fatores devem ser potências de 2, isso só acontece
Logo, só tem solução para
Os números são
Para complemento: Fermat Quotient
Abraço !
Editado pela última vez por Vinisth em 09 Jan 2015, 11:58, em um total de 1 vez.
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última mensagem
-
- 3 Respostas
- 3686 Exibições
-
Última mensagem por willames
-
- 2 Respostas
- 823 Exibições
-
Última mensagem por MeninoNeymar
-
- 3 Respostas
- 2208 Exibições
-
Última mensagem por csmarcelo
-
- 1 Respostas
- 991 Exibições
-
Última mensagem por Ittalo25

