Encontre todos os primos [tex3]p[/tex3]
, para os quais o quociente.
[tex3]\frac{2^{p-1}-1}{p}[/tex3]
é um quadrado perfeito.
Olimpíadas ⇒ Números primos
Moderador: [ Moderadores TTB ]
-
Auto Excluído (ID:12031)

- Última visita: 31-12-69
Jun 2014
19
22:36
Re: Números primos
Cara, não consegui resolver ainda mas vou deixar aqui algumas observações que eu acho que podem ajudar a resolver esse problema:
Se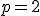 teremos:
teremos:

então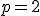 não nos convém.
não nos convém.
Pelo pequeno teorema de fermat se=1) e
e 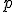 é primo então:
é primo então:
)
Se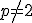 então o pequeno teorema de fermat garante que
então o pequeno teorema de fermat garante que
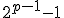 é múltiplo de
é múltiplo de 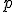
o problema pede que:

como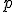 é ímpar podemos dizer que
é ímpar podemos dizer que  é um quadrado perfeito. Pois o expoente é par. Mais do que isso
é um quadrado perfeito. Pois o expoente é par. Mais do que isso  não é divisível por 3. Pois é uma potência de 2.
não é divisível por 3. Pois é uma potência de 2.
Lema: Todo quadrado perfeito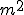 quando dividido por 3 deixa restos:
quando dividido por 3 deixa restos:
1 - se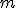 não for múltiplo de 3
não for múltiplo de 3
0 - se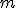 é múltiplo de 3
é múltiplo de 3
Prova: ou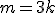 pra
pra  inteiro positivo então
inteiro positivo então )
ou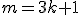 então
então +1)
ou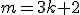 então
então +1)
cqd
então temos que%20%5Crightarrow%20%202%5E%7Bp-1%7D%20-%201%20%5Cequiv%200%5C,%20mod(3)) então devemos ter que:
então devemos ter que:
)
excetuando-se o caso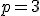 que satisfaz a condição do problema pois:
que satisfaz a condição do problema pois:
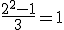
devemos ter então e é fácil ver que
e é fácil ver que 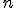 deve ser ímpar, pois
deve ser ímpar, pois 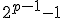 é ímpar e
é ímpar e 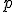 também é. Então
também é. Então ) .
.
Com esta descoberta podemos inferir agora que se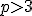 então
então )
observemos que:
)
)
)
)
%5Cequiv%2016%5C,%20mod(9)%20%5Cequiv%207%5C,%20mod(9))
%5Cequiv%205%20%5C,%20mod(9))
%5Cequiv%2010%5C,mod(9)%20%5Cequiv%201%5C,mod(9))
e a partir dai o padrão se repete.
Então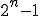 só é divisível por 9 se
só é divisível por 9 se 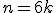 pra algum
pra algum  inteiro não-negativo, então temos que
inteiro não-negativo, então temos que )
teremos:
%5E2)
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 4. Todo quadrado perfeito par é divisível por 4.
Prova: Seja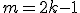 então
então +1)
pra os primos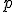 com
com 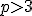 temos que
temos que  é divisível por 4 então:
é divisível por 4 então:
)
do lado direito:
%5E2%20%5Cequiv%20p%5C,mod(4))
então
%20%5Crightarrow%20%20p%20=4x%20+3(**))
) e
e ) :
: 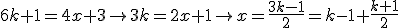
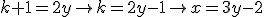
vou só mostrar que deve ser ímpar e deixar indicada a PA em que
deve ser ímpar e deixar indicada a PA em que 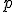 se encontra. Pelo teorema de Dirichlet para progressões aritméticas, temos que existem infinitos primos nessa sequência, então eu não resolvi o problema, mas o restringi um pouco. Espero que isso sirva pra alguém.
se encontra. Pelo teorema de Dirichlet para progressões aritméticas, temos que existem infinitos primos nessa sequência, então eu não resolvi o problema, mas o restringi um pouco. Espero que isso sirva pra alguém.
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 8.
Prova: Seja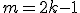 então
então +1)
é fácil ver que) é par.
é par.
pra os primos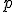 com
com 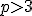 temos que
temos que  é divisível por 8 então:
é divisível por 8 então:
)
do lado direito:
%5E2%20%5Cequiv%20p%5C,mod(8))
então
%20%5Crightarrow%20%20p%20=8z%20+7%20=%204x%20+%203%5Crightarrow%20%20x=2z+1) cqd
cqd
como
 então
então 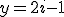
-2)+3%20=4(6i-5)+3=24i-17)
alguns candidatos a solução são: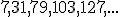
Se
então
Pelo pequeno teorema de fermat se
Se
o problema pede que:
como
Lema: Todo quadrado perfeito
1 - se
0 - se
Prova: ou
ou
ou
cqd
então temos que
excetuando-se o caso
devemos ter então
Com esta descoberta podemos inferir agora que se
observemos que:
e a partir dai o padrão se repete.
Então
teremos:
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 4. Todo quadrado perfeito par é divisível por 4.
Prova: Seja
pra os primos
do lado direito:
então
vou só mostrar que
Lema: todo quadrado perfeito ímpar deixa resto 1 quando dividido por 8.
Prova: Seja
é fácil ver que
pra os primos
do lado direito:
então
como
alguns candidatos a solução são:
Última edição: Auto Excluído (ID:12031) (Qui 19 Jun, 2014 22:36). Total de 1 vez.
-
Auto Excluído (ID:12031)

- Última visita: 31-12-69
Jan 2015
09
11:11
Re: Números primos
logo para todo primo da forma
excetuando-se o caso
Última edição: Auto Excluído (ID:12031) (Sex 09 Jan, 2015 11:11). Total de 1 vez.
Jan 2015
09
11:58
Re: Números primos
Ol,á a todos,
Primeiro faz-se o teste com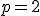 , como sousóeu fez.
, como sousóeu fez.
Todo primo é ímpar, logo seja p da foma
é ímpar, logo seja p da foma (2%5En+1)=(2n+1)x%5E2)
Como=1) e cada fator é um número ímpar consecutivo, a equação se torna em resolver :
e cada fator é um número ímpar consecutivo, a equação se torna em resolver :
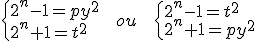
(t+1))
Ambos fatores devem ser potências de 2, isso só acontece

Logo, só tem solução para , analogamente pode-se ter
, analogamente pode-se ter 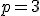 .
.
Os números são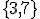
Para complemento: Fermat Quotient
Abraço !
Primeiro faz-se o teste com
Todo primo
Como
Ambos fatores devem ser potências de 2, isso só acontece
Logo, só tem solução para
Os números são
Para complemento: Fermat Quotient
Abraço !
Última edição: Vinisth (Sex 09 Jan, 2015 11:58). Total de 1 vez.
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última msg
-
- 2 Respostas
- 804 Exibições
-
Última msg por MatheusCNIME
-
- 0 Respostas
- 454 Exibições
-
Última msg por MatheusCNIME
-
- 0 Respostas
- 124 Exibições
-
Última msg por Babi123
-
- 5 Respostas
- 375 Exibições
-
Última msg por FelipeMartin
-
- 3 Respostas
- 195 Exibições
-
Última msg por Babi123









