Sabendo que H é o ortocentro do triângulo ABC e que os círculos são tangentes
sempre a um dos lados e a duas alturas distintas.
Provar que os raios a,b,c,d,e,f obedecem a relação: a.b.c = d.e.f
Ensino Médio ⇒ Geometria Plana - Círculos num Triângulo Tópico resolvido
Moderador: [ Moderadores TTB ]
Jan 2012
29
18:50
Geometria Plana - Círculos num Triângulo
Última edição: andreluiz (Dom 29 Jan, 2012 18:50). Total de 1 vez.
-
caju

- Mensagens: 2136
- Registrado em: Qui 19 Out, 2006 15:03
- Última visita: 12-04-24
- Localização: Rio de Janeiro
- Contato:
Fev 2012
02
19:01
Re: Círculos num Triângulo
Olá andreluiz,
Iremos utilizar uma fórmula não muito famigerada, mas de fácil dedução.
É a fórmula do raio do círculo inscrito a um triângulo retângulo
do círculo inscrito a um triângulo retângulo 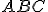 de hipotenusa
de hipotenusa  e catetos
e catetos 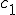 e
e 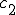 :
:
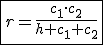
Deixo como exercício a parte da dedução, mas dou uma dica: seja o centro [tex2]P[/tex2] do círculo inscrito, ache a área do triângulo [tex2]ABC[/tex2] utilizando os catetos e ache a área do triângulo [tex2]ABC[/tex2] somando as áreas dos triângulos ABP+BCP+ACP e iguale.
Bom, vamos dar nomes aos segmentos que iremos utilizar na resolução:
Para não poluir muito o desenho, representei os raios dos círculos do desenho do enunciado como sendo a letrinha circulada dentro de cada triângulo.
Agora, com estes valores, podemos encontrar o valor de cada raio com a fórmula apresentada inicialmente:

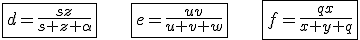
Devemos, também, enxergar algumas semelhanças de triângulo.
Note que os ângulos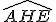 e
e 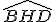 são iguais, pois são OPV (Opostos Pelo Vértice). E, sendo os ângulos
são iguais, pois são OPV (Opostos Pelo Vértice). E, sendo os ângulos 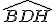 e
e  , temos que os triângulos
, temos que os triângulos 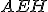 e
e 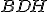 são semelhantes pois possuem todos os ângulos internos iguais.
são semelhantes pois possuem todos os ângulos internos iguais.
Com o mesmo raciocínio, temos que os triângulos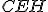 e
e 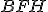 são semelhantes e idem para
são semelhantes e idem para 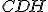 e
e 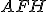 .
.
Com estas três semelhanças, temos:
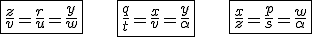
Agora que vem o pulo do gato. Vamos utilizar a propriedade de proporções que diz:
Numa proporção, a soma dos antecedentes está para a soma dos consequentes, assim como cada antecedente está para o seu consequente. Isso quer dizer que se temos uma proporção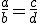 , também é válida a igualdade
, também é válida a igualdade 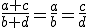
Então vamos aplicar esta propriedade em cada uma das semelhanças que achamos:
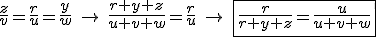

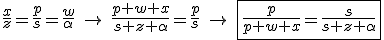
Note que o lado esquerdo das três equações enquadradas acima aparecem nos valores dos raios ,
, 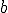 e
e  .
.
Quase acabando, vamos substituir esses três valores acima encontrados, nos resultados obtidos anteriormente para os raios ,
, 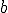 e
e  :
:
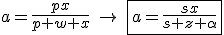
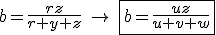
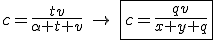
Para finalizar, vamos multiplicar estes valores de ,
, 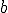 e
e  e vamos comparar com a multiplicação dos valores encontrados anteriormente para
e vamos comparar com a multiplicação dos valores encontrados anteriormente para 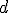 ,
,  e
e 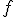 .
.
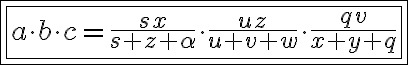
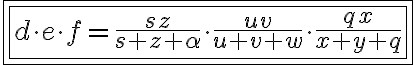
Note que os produtos são iguais. CQD.
Grande abraço,
Prof. Caju
Iremos utilizar uma fórmula não muito famigerada, mas de fácil dedução.
É a fórmula do raio
Deixo como exercício a parte da dedução, mas dou uma dica: seja o centro [tex2]P[/tex2] do círculo inscrito, ache a área do triângulo [tex2]ABC[/tex2] utilizando os catetos e ache a área do triângulo [tex2]ABC[/tex2] somando as áreas dos triângulos ABP+BCP+ACP e iguale.
Bom, vamos dar nomes aos segmentos que iremos utilizar na resolução:
Para não poluir muito o desenho, representei os raios dos círculos do desenho do enunciado como sendo a letrinha circulada dentro de cada triângulo.
Agora, com estes valores, podemos encontrar o valor de cada raio com a fórmula apresentada inicialmente:
Devemos, também, enxergar algumas semelhanças de triângulo.
Note que os ângulos
Com o mesmo raciocínio, temos que os triângulos
Com estas três semelhanças, temos:
Agora que vem o pulo do gato. Vamos utilizar a propriedade de proporções que diz:
Numa proporção, a soma dos antecedentes está para a soma dos consequentes, assim como cada antecedente está para o seu consequente. Isso quer dizer que se temos uma proporção
Então vamos aplicar esta propriedade em cada uma das semelhanças que achamos:
Note que o lado esquerdo das três equações enquadradas acima aparecem nos valores dos raios
Quase acabando, vamos substituir esses três valores acima encontrados, nos resultados obtidos anteriormente para os raios
Para finalizar, vamos multiplicar estes valores de
Note que os produtos são iguais. CQD.
Grande abraço,
Prof. Caju
Última edição: caju (Qui 02 Fev, 2012 19:01). Total de 3 vezes.
"A beleza de ser um eterno aprendiz..."
-
FilipeCaceres

- Mensagens: 2504
- Registrado em: Seg 16 Nov, 2009 20:47
- Última visita: 24-01-20
Fev 2012
08
00:34
Re: Geometria Plana - Círculos num Triângulo
Olá a todos,
Uma outra solução possível.
Veja que o triângulo , assim temos
, assim temos
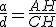
Analogamente,

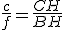
Multiplicando,
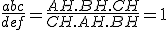
Portanto,
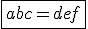 .CQD
.CQD
Abraço.
Uma outra solução possível.
Veja que o triângulo
Analogamente,
Multiplicando,
Portanto,
Abraço.
Última edição: FilipeCaceres (Qua 08 Fev, 2012 00:34). Total de 2 vezes.
-
caju

- Mensagens: 2136
- Registrado em: Qui 19 Out, 2006 15:03
- Última visita: 12-04-24
- Localização: Rio de Janeiro
- Contato:
Fev 2012
08
01:11
Re: Geometria Plana - Círculos num Triângulo
Nossa... muito melhor, Filipe.
Realmente, esqueci desse detalhe. Quando os triângulos são semelhantes, os raios dos círculos inscritos a esses triângulos seguem a proporção de semelhança (idem para o círculo circunscrito).
Muito bom, parabéns!
Grande abraço,
Prof. Caju
Realmente, esqueci desse detalhe. Quando os triângulos são semelhantes, os raios dos círculos inscritos a esses triângulos seguem a proporção de semelhança (idem para o círculo circunscrito).
Muito bom, parabéns!
Grande abraço,
Prof. Caju
"A beleza de ser um eterno aprendiz..."
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última msg
-
- 1 Respostas
- 5574 Exibições
-
Última msg por Carlosft57
-
- 1 Respostas
- 4582 Exibições
-
Última msg por Carlosft57
-
- 1 Respostas
- 4210 Exibições
-
Última msg por Carlosft57
-
- 1 Respostas
- 4633 Exibições
-
Última msg por Carlosft57
-
- 1 Respostas
- 4846 Exibições
-
Última msg por Carlosft57








