Ensino Superior

Mensagem não lidapor **lipemachado** » 09 Mai 2015, 08:57

Calcule a integral usando a coordenadas polares [tex3]\int\limits\int\limits (x+ y )dA[/tex3] onde D; [tex3]x^{2}+y^2 -2y \leq 0[/tex3]

Obs.: Quero saber como eu encontro os intervalos de integração

Mensagem não lidapor **candre** » 09 Mai 2015, 14:02 · Mensagem não lida por **candre** » 09 Mai 2015, 14:02

temos que
$x^2+y^2-2y\le0\\ x^2+y^2-2y+1\le1\\ x^2+(y-1)^2\le1$
temos que a região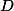 $D$ é um circunferência de raio $1$ centrado em $(0,1)$

pudim

podemos fazer a seguinte mudança de coordenadas
$x=r\cos\theta\\ y=1+r\sin\theta\\ \frac{\partial(x,y)}{\partial(r,\theta)}=r\\ \iint\limits_D(x+y)dA =\iint\limits_D(x+y)\frac{\partial(x,y)}{\partial(r,\theta)}drd\theta =\int\limits_{0}^{2\pi}\int\limits_{0}^{1}(r\cos\theta+1+r\sin\theta)rdrd\theta\\ =\int\limits_{0}^{2\pi}\int\limits_{0}^{1}r^2\cos\theta+r+r^2\sin\theta drd\theta\\ =\int\limits_{0}^{2\pi}\int\limits_{0}^{1}r^2\cos\theta drd\theta+\int\limits_{0}^{2\pi}\int\limits_{0}^{1}rdrd\theta+\int\limits_{0}^{2\pi}\int\limits_{0}^{1}r^2\sin\theta drd\theta\\ =\int\limits_{0}^{2\pi}\cos\theta \int\limits_{0}^{1}r^2drd\theta+\int\limits_{0}^{2\pi}d\theta \int\limits_{0}^{1}rdr+\int\limits_{0}^{2\pi}\sin\theta\int\limits_{0}^{1}r^2 drd\theta\\ =\int\limits_{0}^{2\pi}\cos\theta d\theta\int\limits_{0}^{1}r^2dr+\int\limits_{0}^{2\pi}d\theta \int\limits_{0}^{1}rdr+\int\limits_{0}^{2\pi}\sin\theta d\theta\int\limits_{0}^{1}r^2 dr\\ =0\cdot\frac{1}{3}+2\pi\cdot\frac{1}{2}+0\cdot\frac{1}{3}\\ =\pi$

podemos ver a região no plano $\mathbb{R}^2$ conforme visto figura abaixo

: se prepara pra converter; essa linda tecpix.png (2.77 KiB) Exibido 740 vezes

e circunferência e dada por $x^2+(y-1)^2=1$ , colocando $x=r\cos\theta$ e $y=r\sin\theta$ obtemos
$r^2\cos^2\theta+(r\sin\theta-1)^2=1\\ r^2\cos^2\theta+r^2\sin^2\theta-2r\sin\theta+1=1\\ r^2(\cos^2\theta+\sin^2\theta)-2r\sin\theta=0\\ r^2-2r\sin\theta=0\\ r(r-2\sin\theta)=0\\ r=0\vee r=2\sin\theta$
temos que para $0\le\theta\le\pi\Rightarrow r=2\sin\theta$ já da a circunferência, sendo que $0\le r\le2\sin\theta$ descreve toda a região do interior da circunferência incluindo a própria circunferência e obtemos portanto
$\iint\limits_D(x+y)dA =\iint\limits_D(x+y)\frac{\partial(x,y)}{\partial(r,\theta)}drd\theta =\int\limits_{0}^{\pi}\int\limits_{0}^{2\sin\theta}r(\cos\theta+\sin\theta)rdrd\theta\\ =\int\limits_{0}^{\pi}(\cos\theta+\sin\theta)\int\limits_{0}^{2\sin\theta}r^2drd\theta\\ =\int\limits_{0}^{\pi}(\cos\theta+\sin\theta)\frac{r^3}{3}\bigg|_{0}^{2\sin\theta}d\theta\\ =\frac{8}{3}\int\limits_{0}^{\pi}(\cos\theta+\sin\theta)\sin^3\theta d\theta\\ =\frac{8}{3}\int\limits_{0}^{\pi}\cos\theta\sin^3\theta+\sin^4\theta d\theta\\ =\frac{8}{3}\left(\int\limits_{0}^{\pi}\cos\theta\sin^3\theta d\theta+\int\limits_{0}^{\pi}\sin^4\theta d\theta\right)\\ \int\limits_{0}^{\pi}\cos\theta\sin^3\theta d\theta=\int\limits_{0}^{0}u^3du=0\\ u=\sin\theta\\ du=\cos\theta d\theta\\ \theta=0\Rightarrow u=0\\ \theta=\pi\Rightarrow u=0\\ \text{usando recorrencia para a funcao seno na proxima}\\ \int\limits_{0}^{\pi}\sin^4\theta d\theta= \overbrace{-\frac{\sin^3\theta\cos\theta}{4}\bigg|_{0}^{\pi}}^{0}+\frac{3}{4}\int\limits_{0}^{\pi}\sin^2\theta d\theta\\ =\frac{3}{4}\left(\underbrace{-\frac{\sin\theta\cos\theta}{2}\bigg|_{0}^{\pi}}_{0}+\frac{1}{2}\int\limits_{0}^{\pi}d\theta\right)=\frac{3\pi}{8}\\ \iint\limits_D(x+y)dA=\frac{8}{3}\cdot\frac{3\pi}{8}=\pi$

Mensagem não lidapor **lipemachado** » 09 Mai 2015, 21:03

Muito Obrigado!!!

Mas por que [tex3]\theta[/tex3] está variando [tex3]0 \leq \theta \leq \pi[/tex3] ?

Mensagem não lidapor **candre** » 10 Mai 2015, 15:38 · Mensagem não lida por **candre** » 10 Mai 2015, 15:38

lipemachado escreveu:Muito Obrigado!!!

Mas por que [tex3]\theta[/tex3]
Código: Selecionar tudoSHIFT+Click na eq = ZOOM
[tex3]\theta[/tex3]
está variando [tex3]0 \leq \theta \leq \pi[/tex3]
Código: Selecionar tudoSHIFT+Click na eq = ZOOM
[tex3]0 \leq \theta \leq \pi[/tex3]
?

utilizando a figura abaixo para explicar

: figura explicativa; voce quer brinca na neve.png (17.69 KiB) Exibido 733 vezes

em coordenada polares usamos as coordenadas $(r,\theta)$ para representar um ponto, onde $r$ e a distancia ate a origem e $\theta$ e o angulo entre o vetor posição e o eixo $x$ medido no sentido anti horário.
partino para a construção do gráfico, pegamos uma reta orientada com um angulo $\theta$ , e a cada angulo $\theta$ colocamos seu correspondente $r$ nela, e fazemos isso para todo os ângulos, como a função seno e $2\pi$ periódica então obviamente não pegar todos os valores de $\theta$ em $[0,2\pi]$ já e suficiente (claro que na pratica ninguém pega infinitos pontos, apenas uma quantidade suficiente para fazer um bom gráfico), observando o gráfico a função em $[\pi,2\pi]$ se comporta que nem em $[0,\pi]$ só que em vez de ser positiva e negativa.
plotando nosso gráfico, vamos separar em dois casos
para [tex2]0\le\theta\le\pi[/tex2]
começamos com $r$ zerado em $\theta=0=0^\circ$ ,ele vai aumentando ate chegar no seu valor máximo em $\theta=\frac{\pi}{2}=90^\circ$ , depois disso ela vai diminuir ate zerar em $\theta=\pi=180^\circ$ , nisso já temos a nossa circunferência (ou nossa região se no processo fossemos colorindo onde a região da reta que esta entre $0$ e nosso ponto azul passa).
para [tex2]\pi\le\theta\le2\pi[/tex2]
começamos com $r$ zerado em $\theta=\pi=180^\circ$ , porem ele vai diminuindo ate chegar no seu valor minimo em $\theta=\frac{3\pi}{2}=270^\circ$ , onde o valor e negativo e depois vai aumentando ate zerar em $\theta=2\pi=360^\circ$ , mas antes que alguém pergunte, sim, esses valores são negativos, mas como plotamos? simples, observe que pegamos uma reta orientada, se fosse por exemplo em um eixo unidimensional, quando o valor e negativo ele estaria no outro lado do centro do eixo, de forma análoga funciona aqui, então nessa região, ao invés de ir plotando esses valores de $r$ na direção positiva, plotamos eles na direção negativa (que seria a região tracejada da reta), as se você reparar bem pelo comportamento da função, vai reparar que o que você vai obter e novamente a circunferência, ou seja, em uma volta completa obtemos a mesma circunferência duas vezes, por isso usamos $\theta$ variando de $0$ a $\pi$ , pois se usamos $\theta$ variando de $0$ a $2\pi$ estaremos passando por duas vezes na mesma região, obtendo um valor igual ao dobro do esperado.

Ensino Superior ⇒ Integração em coordenadas polares

Integração em coordenadas polares

Re: Integração em coordenadas polares

Re: Integração em coordenadas polares

Re: Integração em coordenadas polares

Ensino Superior ⇒ Integração em coordenadas polares

Integração em coordenadas polares

Re: Integração em coordenadas polares

Re: Integração em coordenadas polares

Re: Integração em coordenadas polares

Entrar | Registrar