Página 1 de 1
Derivada: Equação da reta tangente
Enviado: Seg 03 Out, 2016 18:50
por carolzinhag3
Encontre as equações para as retas que são tangentes a elipse
![\ \frac{x^2}{4}+ y^2 =1\](https://www.tutorbrasil.com.br/latex/mimetex_.cgi?\ \frac{x^2}{4}+ y^2 =1\ "\ \frac{x^2}{4}+ y^2 =1\")
e passam pelo ponto (0,2)
*se puderem explicar de forma detalhada, ficarei grata.
Re: Derivada: Equação da reta tangente
Enviado: Ter 04 Out, 2016 00:24
por LucasPinafi
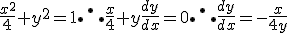
Assim, a equação da reta tangente à elipse no ponto (x,y) é:
 "Y - y = - \frac{x}{4y} (X-x)")
(veja que usei X no papel de x, e x no lugar de
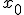
para não carregar a notação). Porém, sabemos que
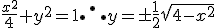
Consideremos apenas a parte positiva (porquê?)
 "Y - \frac 1 2 \sqrt{4-x^2} = - \frac{x}{2\sqrt{4-x^2}} (X-x)")
. Porém, a reta deve passar pelo ponto (0,2). Assim,
 \therefore 2 = \frac{x^2}{2\sqrt{4-x^2}} + \frac{1}{2}\sqrt{4-x^2} \\ \frac{x^2 + 4 - x^2}{2\sqrt{4-x^2}} = 2 \therefore \frac{2}{\sqrt{4-x^2}} =2 \therefore \sqrt{4-x^2} = 1 \therefore 4-x^2 = 1 \\ x^2 = 3 \therefore x = \pm \sqrt 3 "2 - \frac{1}{2}\sqrt{4- x^2} = - \frac{x}{2\sqrt{4 - x^2} }(0-x) \therefore 2 = \frac{x^2}{2\sqrt{4-x^2}} + \frac{1}{2}\sqrt{4-x^2} \\ \frac{x^2 + 4 - x^2}{2\sqrt{4-x^2}} = 2 \therefore \frac{2}{\sqrt{4-x^2}} =2 \therefore \sqrt{4-x^2} = 1 \therefore 4-x^2 = 1 \\ x^2 = 3 \therefore x = \pm \sqrt 3")
Assim, temos que
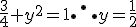
. As retas são:
 "y - \frac{1}{2} = \frac{\sqrt 3}{2} (x +\sqrt 3)")
e
 "y - \frac{1}{2} = - \frac{\sqrt 3 x}{2} (x - \sqrt 3 )")
Re: Derivada: Equação da reta tangente
Enviado: Ter 04 Out, 2016 14:35
por carolzinhag3
desculpa a ignorância, mas na primeira linha a derivada de x² e y² não deveria ser 2x e 2y, respectivamente?
Re: Derivada: Equação da reta tangente
Enviado: Qui 13 Out, 2016 15:32
por ALEXZOE
Colega, vc poderia explicar o motivo de considerar apenas a parte positiva do valor de y.
obg.
Re: Derivada: Equação da reta tangente
Enviado: Qui 13 Out, 2016 15:57
por ALEXZOE
entendi... desenvolvendo para o b negativo não pertence a R (conjunto dos reais). MAS, como passam pelo ponto (0,2), elas não devem ser da forma:
 = m (x - 0) "(y - 2) = m (x - 0)")
, onde m é o coeficiente angular?
Assim, achei as seguintes equações:
 = - \frac{\sqrt 3}{2} (x - 0) "(y - 2) = - \frac{\sqrt 3}{2} (x - 0)")
e
 = \frac{\sqrt 3}{2} (x - 0) "(y - 2) = \frac{\sqrt 3}{2} (x - 0)")
.
E AGORA?
Re: Derivada: Equação da reta tangente
Enviado: Qui 13 Out, 2016 23:20
por LucasPinafi
mano, são as mesmas equações q as minhas kkk dá uma olhada
Re: Derivada: Equação da reta tangente
Enviado: Qui 13 Out, 2016 23:24
por ALEXZOE
verdade... Que coisa... Kkkk....
Vida que segue....