Como resolver usando derivadas?
Ensino Superior ⇒ (UEL) Geometria Analítica Tópico resolvido
Moderador: [ Moderadores TTB ]
Jun 2016
27
17:35
(UEL) Geometria Analítica
Seja a parábola de equação  . As equações das retas tangentes ao gráfico da parábola que passam pelo ponto
. As equações das retas tangentes ao gráfico da parábola que passam pelo ponto 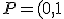 ) são:
) são:
Como resolver usando derivadas?
Como resolver usando derivadas?
Última edição: brunoafa (Seg 27 Jun, 2016 17:35). Total de 2 vezes.
MACTE ANIMO! GENEROSE PUER, SIC ITUR AD ASTRA
-
LucasPinafi

- Mensagens: 1765
- Registrado em: Dom 07 Dez, 2014 00:08
- Última visita: 11-04-24
Jun 2016
27
18:07
Re: UEL Geometria Analítica
Usando derivadas
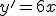
Equação da reta tangente no ponto (x,y)
%20(X-x)%20%5Ctherefore%20Y-y%20=%206x(X-x))
Como passa por P(0, 1),
%20%5Ctherefore%206x%5E2%20=y-1)
Mas,
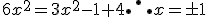
Coeficiente angular,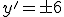
Equação da reta: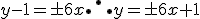
Equação da reta tangente no ponto (x,y)
Como passa por P(0, 1),
Mas,
Coeficiente angular,
Equação da reta:
Última edição: LucasPinafi (Seg 27 Jun, 2016 18:07). Total de 1 vez.
Ser ̶m̶e̶l̶h̶o̶r̶ pior a cada dia
Jun 2016
27
18:37
Re: UEL Geometria Analítica
Eu achei que o coeficiente angular seria 0.
O que é esse X??
O que é esse X??
Última edição: brunoafa (Seg 27 Jun, 2016 18:37). Total de 1 vez.
MACTE ANIMO! GENEROSE PUER, SIC ITUR AD ASTRA
-
LucasPinafi

- Mensagens: 1765
- Registrado em: Dom 07 Dez, 2014 00:08
- Última visita: 11-04-24
Jun 2016
27
19:18
Re: UEL Geometria Analítica
Geometricamente, você já poderia descartar esse pensamento.
(X,Y) é o conjunto de pontos da reta:
y-y0 = m(x-x0)
ao em vez de usar x0 e y0, usei x e y (isso facilita problemas que você eventualmente encontrará em equações diferenciais) e X e Y em vez de x e y. Apenas uma questão de notação.
(X,Y) é o conjunto de pontos da reta:
y-y0 = m(x-x0)
ao em vez de usar x0 e y0, usei x e y (isso facilita problemas que você eventualmente encontrará em equações diferenciais) e X e Y em vez de x e y. Apenas uma questão de notação.
Ser ̶m̶e̶l̶h̶o̶r̶ pior a cada dia
Jun 2016
27
19:49
Re: UEL Geometria Analítica
Ah tá, entendi agora.
Valeu cara! Não manjo de cálculo ainda, só sei essa regrinha de "abaixar" os expoentes e multiplicar mesmo, não sei de onde saiu, vou dar uma olhada depois.
Valeu cara! Não manjo de cálculo ainda, só sei essa regrinha de "abaixar" os expoentes e multiplicar mesmo, não sei de onde saiu, vou dar uma olhada depois.
MACTE ANIMO! GENEROSE PUER, SIC ITUR AD ASTRA
-
LucasPinafi

- Mensagens: 1765
- Registrado em: Dom 07 Dez, 2014 00:08
- Última visita: 11-04-24
Jun 2016
27
21:32
Re: UEL Geometria Analítica
Fiz um textinho aqui...heaueha Estou treinando um pouco para o futuro. Para quem faz vestibular militar, esse tipo de conhecimento básico sobre cálculo é uma grande (grande mesmo) vantagem.
De onde saiu:
Bem, embora o cálculo seja uma matéria de nível superior, alguns conceitos básicos podem ser aprendido por quem tem um nível médio bom - não precisa nem ser excelente.
A ideia de derivada provém da ideia de variação: dada uma função f(x), uma pergunta que surge naturalmente é: como f varia quando variamos x? Essa resposta é dada pela derivada. De modo bem superficial, a variação média de f quando x varia de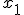 até
até 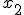 é dada pela razão incremental:
é dada pela razão incremental:
%20-%20f(x_1)%7D%7Bx_2%20-%20x_1%7D) Geometricamente,
Geometricamente, 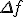 é o coeficiente angular da reta que passa pelos pontos
é o coeficiente angular da reta que passa pelos pontos )) e
e )) . Essa reta é uma reta secante ao gráfico de f. Fazendo com que
. Essa reta é uma reta secante ao gráfico de f. Fazendo com que 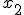 se aproxime cada vez mais de
se aproxime cada vez mais de 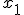 , a reta secante vai ficando cada vez mais mais "tangente" ao gráfico. Assim, no limite em que
, a reta secante vai ficando cada vez mais mais "tangente" ao gráfico. Assim, no limite em que 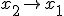 , ou seja, quando
, ou seja, quando 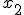 é muito próximo de
é muito próximo de 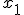 , porém sem ser igual a
, porém sem ser igual a 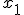 , teremos a taxa de variação instantânea de f. Essa é a derivada, e escrevemos:
, teremos a taxa de variação instantânea de f. Essa é a derivada, e escrevemos:
%20=%5Clim_%7Bx_2%20%5Cto%20x_1%7D%20%5Cfrac%7Bf(x_2)%20-%20f(x_1)%7D%7Bx_2%20-x_1%7D) onde o símbolo ' representa a derivada. Você também pode encontrar uma notação mais usual e útil,
onde o símbolo ' representa a derivada. Você também pode encontrar uma notação mais usual e útil, 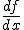 .
.
Em palavras: a taxa de variação instantânea de f no ponto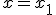 é igual ao limite da razão incremental. Em termos geométricos,
é igual ao limite da razão incremental. Em termos geométricos, 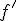 é o coeficiente angular da reta tangente no ponto
é o coeficiente angular da reta tangente no ponto )) .
.
==================================================================================================
Propriedades da derivada
Nessa discussão, é suficiente saber que:
1) A derivada de uma soma é a soma das derivadas, isso é,'(x)%20=f'(x)%20+%20g'(x))
2) O produto de uma derivada é igual a:'(x)%20=%20f'(x)%20g(x)%20+%20f(x)%20g'(x))
3) O quociente de uma derivada é igual a:![\left(\frac{f}{g}\right)'(x) = \frac{f'(x) g(x) - f(x) g'(x)}{[g(x)]^2} \left(\frac{f}{g}\right)'(x) = \frac{f'(x) g(x) - f(x) g'(x)}{[g(x)]^2}](https://www.tutorbrasil.com.br/latex/mimetex_.cgi?%5Cleft(%5Cfrac%7Bf%7D%7Bg%7D%5Cright)'(x)%20=%20%5Cfrac%7Bf'(x)%20g(x)%20-%20f(x)%20g'(x)%7D%7B%5Bg(x)%5D%5E2%7D) , desde que
, desde que %20%5Cneq%200) para todo x.
para todo x.
4) A derivada de uma constante é nula.
==================================================================================================
Portanto, utilizando a propriedade 1, 2 e 4 podemos facilmente calcular a derivada de um polinômio. Seja:
%20=%20a_0%20+%20a_1%20x+a_2%20x%5E2%20+%20%5Ccdots%20+%20a_nx%5En) Então,
Então,
%20=%20(a_0%20+%20a_1%20x%20+a_2%20x%5E2%20+%20%5Ccdots%20+%20a_n%20x%5En)') e, pela propriedade 1:
e, pela propriedade 1:
%20=%20(a_0)'%20+%20(a_1x)'%20+%20(a_2%20x%5E2)'%20+%20%5Ccdots%20+%20(a_n%20x%5En)') Pela propriedade 4,
Pela propriedade 4, '=0) , e pela propriedade 2,
, e pela propriedade 2, '%20=a_n%20(x%5En)'%20+a_n'%20x%5En) , mas
, mas 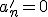 , de modo que
, de modo que '%20=%20a_n%20(x_n)') . Portanto, nos resta o trabalho de calcular a derivada
. Portanto, nos resta o trabalho de calcular a derivada ') . Pela própria definição de derivada:
. Pela própria definição de derivada:
%20=%20%5Clim_%7B%20x%20%5Cto%20x_0%7D%20%5Cfrac%7Bx%5En%20-%20x_0%5En%7D%7Bx-x_0%7D) mas,
mas, %20(x%5E%7Bn-1%7D%20+%20x%5E%7Bn-2%7D%20x_0+%20%5Ccdots%20+%20x%5Ccdot%20x_0%5E%7Bn-2%7D+x_0%5E%7Bn-1%7D)) , e portanto:
, e portanto:
%20=%20%5Cfrac%7B(x-x_0)%20(x%5E%7Bn-1%7D%20+%20x%5E%7Bn-2%7D%20x_0%20+%20%5Ccdots%20+%20x%20%5Ccdot%20x_0%5E%7Bn-2%7D%20+%20x_0%5E%7Bn-1%7D)%7D%7Bx-x_0%7D) e, como
e, como  se aproxima de
se aproxima de 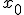 , mas nunca são iguais, segue que podemos simplificar o numerador com o denominador e obter
, mas nunca são iguais, segue que podemos simplificar o numerador com o denominador e obter %20=%20%5Clim_%7Bx%5Cto%20x_0%7D%20(x%5E%7Bn-1%7D%20+%20x%5E%7Bn-2%7D%20x_0%20+%20%5Ccdots%20+x%20%5Ccdot%20x_0%5E%7Bn-2%7D%20+%20x_0%5E%7Bn-1%7D)) , portanto, para
, portanto, para 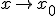 , cada um desses termos é igual a
, cada um desses termos é igual a 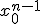 , e como há n termos:
, e como há n termos:
'%20=%20n%5Ccdot%20a_n%5Ccdot%20x%5E%7Bn-1%7D) Portanto,
Portanto,
%20=%20a_1%20+%202a_2%20x+%203a_3%20x%5E2%20+%20%5Ccdot%20+%20n%5Ccdot%20a_n%20%5Ccdot%20x%5E%7Bn-1%7D)
De onde saiu:
Bem, embora o cálculo seja uma matéria de nível superior, alguns conceitos básicos podem ser aprendido por quem tem um nível médio bom - não precisa nem ser excelente.
A ideia de derivada provém da ideia de variação: dada uma função f(x), uma pergunta que surge naturalmente é: como f varia quando variamos x? Essa resposta é dada pela derivada. De modo bem superficial, a variação média de f quando x varia de
Em palavras: a taxa de variação instantânea de f no ponto
==================================================================================================
Propriedades da derivada
Nessa discussão, é suficiente saber que:
1) A derivada de uma soma é a soma das derivadas, isso é,
2) O produto de uma derivada é igual a:
3) O quociente de uma derivada é igual a:
4) A derivada de uma constante é nula.
==================================================================================================
Portanto, utilizando a propriedade 1, 2 e 4 podemos facilmente calcular a derivada de um polinômio. Seja:
Última edição: LucasPinafi (Seg 27 Jun, 2016 21:32). Total de 1 vez.
Ser ̶m̶e̶l̶h̶o̶r̶ pior a cada dia
Jun 2016
28
11:39
Re: (UEL) Geometria Analítica
Cara, obrigado por ter gastado seu tempo me ajudando a entender a matéria. Realmente, acredito que o conhecimento de limites e derivadas é algo que ajuda muito, já tive uma aula sobre noções básicas de cálculo mas acaba ficando tudo muito "jogado" e não consigo entender as aplicações daquilo que estudei.
Só um adendo, na "notação usual" ao invés de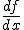 não seria
não seria 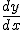 ?
?
Consegui entender um pouco da onde saiu a regra de abaixar os coeficientes (obrigado! rs) mas ainda estou na dúvida, para que serve derivar um polinômio?
Até onde eu entendi de tudo que vi de derivadas, derivar seria achar o coeficiente angular de uma reta, a taxa de variação como você falou. Por isso que no caso do problema que postei é util para achar a reta tangente no ponto dado, mas e em outro casos?
Só um adendo, na "notação usual" ao invés de
Consegui entender um pouco da onde saiu a regra de abaixar os coeficientes (obrigado! rs) mas ainda estou na dúvida, para que serve derivar um polinômio?
Até onde eu entendi de tudo que vi de derivadas, derivar seria achar o coeficiente angular de uma reta, a taxa de variação como você falou. Por isso que no caso do problema que postei é util para achar a reta tangente no ponto dado, mas e em outro casos?
Última edição: brunoafa (Ter 28 Jun, 2016 11:39). Total de 2 vezes.
MACTE ANIMO! GENEROSE PUER, SIC ITUR AD ASTRA
-
LucasPinafi

- Mensagens: 1765
- Registrado em: Dom 07 Dez, 2014 00:08
- Última visita: 11-04-24
Jun 2016
28
12:37
Re: UEL Geometria Analítica
A derivada representa a taxa de variação instantânea. Darei exemplos simples. Não vou fazer as contas, pois quero que você entenda apenas a ideia por trás da derivada.
Exemplo Considere uma esfera de raio R. Suponha que o raio R da esfera cresce a uma taxa constante de M metros por segundo. Uma pergunta que surge naturalmente. Qual a taxa de variação do volume da esfera?
Pense um pouco sobre esse problema. O que ele nos informa é a taxa de variação de R com t, ou seja, ele nos informa que:
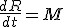 E pede para calcularmos a taxa de variação do volume com o tempo, ou seja,
E pede para calcularmos a taxa de variação do volume com o tempo, ou seja, 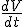 .
.
Interpretação física da derivada: talvez não há nada melhor que uma interpretação física para entendermos um conceito novo. Considere um móvel que se move ao longo do eixo x. A posição desse móvel é monitorada a cada instante. Suponha que no instante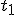 ele esteja na posição
ele esteja na posição ) e no instante
e no instante 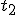 na posição
na posição ) . A velocidade média entre esses pontos é:
. A velocidade média entre esses pontos é:
%20-%20s(t_1)%7D%7Bt_2-t_1%7D) Essa velocidade nada nos diz sobre as características do movimento: nos diz apenas que para percorrer a distância
Essa velocidade nada nos diz sobre as características do movimento: nos diz apenas que para percorrer a distância -s(t_1)) no intervalo de tempo
no intervalo de tempo 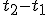 deveríamos percorrer o percurso, com velocidade constante, igual à velocidade média. Porém, e se quisermos resgatar essas informações? Pode ter havido um momento em que o móvel tenha parado, aumentado ou diminuído sua velocidade. Para termos essa informação, devemos saber a velocidade em cada ponto do percurso, ou seja, devemos obter a velocidade instantânea em cada ponto - ou simplesmente a velocidade do móvel. Mas como fazemos isso? Simples! Basta fazer com que o ponto
deveríamos percorrer o percurso, com velocidade constante, igual à velocidade média. Porém, e se quisermos resgatar essas informações? Pode ter havido um momento em que o móvel tenha parado, aumentado ou diminuído sua velocidade. Para termos essa informação, devemos saber a velocidade em cada ponto do percurso, ou seja, devemos obter a velocidade instantânea em cada ponto - ou simplesmente a velocidade do móvel. Mas como fazemos isso? Simples! Basta fazer com que o ponto 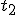 se aproxime cada vez mais de
se aproxime cada vez mais de 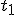 , até que eles fiquem muito próximos. Percebeu a relação com que expliquei acima? Então:
, até que eles fiquem muito próximos. Percebeu a relação com que expliquei acima? Então:
%20=%20%5Clim_%7Bt%20%5Cto%20t_0%7D%20%5Cfrac%7Bs(t)%20-%20s(t_0)%7D%7Bt-t_0%7D=s'(t_0)) (a última igualdade decorre diretamente da definição de derivada)
(a última igualdade decorre diretamente da definição de derivada)
Portanto, a velocidade é a derivada da posição. Ou seja, a derivada representa a velocidade com que uma grandeza varia - tal velocidade pode ser relação ao tempo ou qualquer outra grandeza que esteja também variando.
Pergunta: O que representa a derivada da velocidade) , ou seja, qual significado físico de
, ou seja, qual significado físico de ) ?
?
Exemplo Considere uma esfera de raio R. Suponha que o raio R da esfera cresce a uma taxa constante de M metros por segundo. Uma pergunta que surge naturalmente. Qual a taxa de variação do volume da esfera?
Pense um pouco sobre esse problema. O que ele nos informa é a taxa de variação de R com t, ou seja, ele nos informa que:
Interpretação física da derivada: talvez não há nada melhor que uma interpretação física para entendermos um conceito novo. Considere um móvel que se move ao longo do eixo x. A posição desse móvel é monitorada a cada instante. Suponha que no instante
Portanto, a velocidade é a derivada da posição. Ou seja, a derivada representa a velocidade com que uma grandeza varia - tal velocidade pode ser relação ao tempo ou qualquer outra grandeza que esteja também variando.
Pergunta: O que representa a derivada da velocidade
Última edição: LucasPinafi (Ter 28 Jun, 2016 12:37). Total de 1 vez.
Ser ̶m̶e̶l̶h̶o̶r̶ pior a cada dia
Jun 2016
28
15:19
Re: (UEL) Geometria Analítica
A derivada da velocidade é a aceleração (já sabia dessa! rs)
Agora consegui compreender um pouco melhor o conceito da derivada.
Mas fiquei curioso com o problema da esfera que tem um raio crescente. Eu sei que o volume da esfera é dado por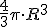 então com certeza o volume cresceria de forma exponencial muito mais rápido do que o raio. Mas como colocar isso em função de M?
então com certeza o volume cresceria de forma exponencial muito mais rápido do que o raio. Mas como colocar isso em função de M?
E outra, por que a derivada do cosseno é o seno e vice versa?
Agora consegui compreender um pouco melhor o conceito da derivada.
Mas fiquei curioso com o problema da esfera que tem um raio crescente. Eu sei que o volume da esfera é dado por
E outra, por que a derivada do cosseno é o seno e vice versa?
Última edição: brunoafa (Ter 28 Jun, 2016 15:19). Total de 1 vez.
MACTE ANIMO! GENEROSE PUER, SIC ITUR AD ASTRA
-
LucasPinafi

- Mensagens: 1765
- Registrado em: Dom 07 Dez, 2014 00:08
- Última visita: 11-04-24
Jun 2016
30
12:28
Re: (UEL) Geometria Analítica
Cuidado ao confundir exponencial com potência !!! A questão da esfera depende de um teorema que é conhecido como regra da cadeia. Não entrarei em detalhes, mas em geral, podemos escrever que:
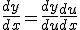 Apresento a solução abaixo.
Apresento a solução abaixo.
%20=4%5Cpi%20MR%5E2) Esse resultado é intuitivo, pois é como se o volume fosse crescendo com as cascas esféricas para cada pequeno aumento do raio R.
Esse resultado é intuitivo, pois é como se o volume fosse crescendo com as cascas esféricas para cada pequeno aumento do raio R.
Em relação a derivada do seno, por definição:
%20'(x_0)%20=%5Clim_%7B%20x%20%5Cto%20x_0%7D%20%5Cfrac%7B%5Csin%20x%20-%20%5Csin%20x_0%7D%7Bx-x_0%7D) Como:
Como: %20%5Ccos%20%5Cleft(%20%5Cfrac%7Bx+x_0%7D%7B2%7D%5Cright)) , segue que:
, segue que:
%20'%20(x_0)%20%20=%5Clim_%7Bx%20%5Cto%20x_0%7D%20%5Cfrac%7B%20%5Csin%20%5Cleft(%5Cfrac%7Bx-x_0%7D%7B2%7D%20%5Cright)%20%5Ccos%20%5Cleft(%20%5Cfrac%7Bx+x_0%7D%7B2%7D%20%5Cright)%7D%7B%5Cfrac%7Bx-x_0%7D%7B2%7D%7D) Para facilitar a notação, façamos
Para facilitar a notação, façamos 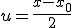 . Veja que, quando x se aproxima cada vez mais de
. Veja que, quando x se aproxima cada vez mais de 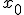 , u vai se aproximando cada vez mais de 0. Logo, no limite, escrevemos u tendendo a zero:
, u vai se aproximando cada vez mais de 0. Logo, no limite, escrevemos u tendendo a zero:
'%20(x_0)%20=%20%5Clim_%7Bu%20%5Cto%200%7D%5Cfrac%7B%5Csin%20u%20%5Ccdot%20%5Ccos%20(2u+x_0)%20%5Cleft%7D%7Bu%7D) Pelas propriedades operatórias dos limites, o limite de um produto é o produto dos limites. Assim,
Pelas propriedades operatórias dos limites, o limite de um produto é o produto dos limites. Assim,
'%20(x_0)%20=%20%5Clim_%7Bu%20%5Cto%200%7D%20%5Ccos%20(2u+x_0)%20%5Ccdot%20%5Clim_%7Bu%20%5Cto%200%7D%20%5Cfrac%7B%5Csin%20u%7D%7Bu%7D) O primeiro desses limites é simples. Quando u tende a zero, temos que o argumento do cosseno vai tendendo cada vez mais para
O primeiro desses limites é simples. Quando u tende a zero, temos que o argumento do cosseno vai tendendo cada vez mais para 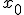 , assim
, assim %20=%20%5Ccos%20x_0) . Já o outro limite requer um pouco mais de atenção. Quando u tende a zero, tanto o numerador quanto o denominador tende a zero. Mas com que "rapidez"? Se o numerador estiver indo para zero mais rapidamente do que o denominador, o limite será zero. Se o denominador estiver indo para zero mais rapidamente, é como se estivéssemos dividindo por zero... logo o resultado não seria um número. Se for na mesma velocidade, dará algum número não nulo. Para não estender no assunto, vamos verificar qual o valor do quociente
. Já o outro limite requer um pouco mais de atenção. Quando u tende a zero, tanto o numerador quanto o denominador tende a zero. Mas com que "rapidez"? Se o numerador estiver indo para zero mais rapidamente do que o denominador, o limite será zero. Se o denominador estiver indo para zero mais rapidamente, é como se estivéssemos dividindo por zero... logo o resultado não seria um número. Se for na mesma velocidade, dará algum número não nulo. Para não estender no assunto, vamos verificar qual o valor do quociente /x) para x pequeno:
para x pequeno:
%7D%7B0.1%7D=%200,9983%20%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cfrac%7B%5Csin%20(0.01)%7D%7B0.01%7D=0,999983%20%20%5C%20%5C%20%5C%20%5C%20%5Cfrac%7B%5Csin%20(0.001)%7D%7B0.001%7D=0,9999..) Parece então que, quando x tende a zero,
Parece então que, quando x tende a zero, 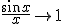 , ou seja, o quociente tende para 1. De fato, esse resultado é verdadeiro e pode ser efetivamente provado, porém isso é complicado. Com tal resultado em mãos, temos que:
, ou seja, o quociente tende para 1. De fato, esse resultado é verdadeiro e pode ser efetivamente provado, porém isso é complicado. Com tal resultado em mãos, temos que:
'%20(x_0)%20=%20%5Ccos%20(x_0))
Resposta
Em relação a derivada do seno, por definição:
Última edição: LucasPinafi (Qui 30 Jun, 2016 12:28). Total de 1 vez.
Ser ̶m̶e̶l̶h̶o̶r̶ pior a cada dia
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última msg
-
- 2 Respostas
- 277 Exibições
-
Última msg por petras
-
- 0 Respostas
- 544 Exibições
-
Última msg por LadyGodiva
-
- 2 Respostas
- 1089 Exibições
-
Última msg por Jigsaw
-
- 0 Respostas
- 882 Exibições
-
Última msg por Lars
-
- 1 Respostas
- 2876 Exibições
-
Última msg por carlosaugusto








