Maratonas de Física ⇒ II Maratona de Física IME/ITA
Moderador: [ Moderadores TTB ]
Set 2012
11
10:04
Re: II Maratona de Física IME/ITA
[tex3]T_1-T_2=m\frac{v_1^2}{R}[/tex3]
e [tex3]T_2=m\frac{v_2^2}{(2R)}[/tex3]
Dividindo a primeira pela segunda temos
[tex3]\frac{T_1}{T_2}-1=\left(\frac{v_1^2}{R}\right)\left(\frac{2R}{v_2^2}\right)[/tex3]
que leva a
[tex3]\frac{T_1}{T_2}=\frac{2v_1^2}{v_2^2}+1[/tex3]
que é a letra A: [tex3]\frac{T_1}{T_2}=\frac{2v_1^2+v_2^2}{v_2^2}[/tex3]
Problema 154
(EN-1994) Em uma repetição da experiência de Young, usando luz monocromática, um estudante verificou que os dois orifícios estão separados de a = 0,1 mm e que as franjas de interferência são observadas em um anteparo situado a uma distância d = 65 cm dos orifícios. Medindo a separação entre duas franjas brilhantes consecutivas, ele encontrou [tex3]\Delta x=0,35cm[/tex3] . Sabe-se que a velocidade de propagação de luz no ar é [tex3]V=3\cdot 10^8 m/s[/tex3] . A freqüência da luz monocromática utilizada nesta experiência, em Hz, é aproximadamente:
a) [tex3]4,6\cdot 10^{14}[/tex3]
b) [tex3]5,3\cdot 10^{14}[/tex3]
c) [tex3]5,6\cdot 10^{4}[/tex3]
d) [tex3]6,3\cdot 10^{4}[/tex3]
e) [tex3]6,7\cdot 10^{4}[/tex3]
Dividindo a primeira pela segunda temos
[tex3]\frac{T_1}{T_2}-1=\left(\frac{v_1^2}{R}\right)\left(\frac{2R}{v_2^2}\right)[/tex3]
que leva a
[tex3]\frac{T_1}{T_2}=\frac{2v_1^2}{v_2^2}+1[/tex3]
que é a letra A: [tex3]\frac{T_1}{T_2}=\frac{2v_1^2+v_2^2}{v_2^2}[/tex3]
Problema 154
(EN-1994) Em uma repetição da experiência de Young, usando luz monocromática, um estudante verificou que os dois orifícios estão separados de a = 0,1 mm e que as franjas de interferência são observadas em um anteparo situado a uma distância d = 65 cm dos orifícios. Medindo a separação entre duas franjas brilhantes consecutivas, ele encontrou [tex3]\Delta x=0,35cm[/tex3] . Sabe-se que a velocidade de propagação de luz no ar é [tex3]V=3\cdot 10^8 m/s[/tex3] . A freqüência da luz monocromática utilizada nesta experiência, em Hz, é aproximadamente:
a) [tex3]4,6\cdot 10^{14}[/tex3]
b) [tex3]5,3\cdot 10^{14}[/tex3]
c) [tex3]5,6\cdot 10^{4}[/tex3]
d) [tex3]6,3\cdot 10^{4}[/tex3]
e) [tex3]6,7\cdot 10^{4}[/tex3]
Última edição: Radius (Ter 11 Set, 2012 10:04). Total de 2 vezes.
-
theblackmamba

- Mensagens: 3723
- Registrado em: Ter 23 Ago, 2011 15:43
- Última visita: 20-11-19
- Localização: São Paulo - SP
Set 2012
11
17:46
Re: II Maratona de Física IME/ITA
Solução do Problema 154
http://www.tutorbrasil.com.br/forum/vie ... 97&p=62169&
----------------------
Problema 155
(AFA - 2008) A figura abaixo apresenta dois corpos de massa [tex3]m[/tex3] suspensos por fios ideais que passam por roldanas também ideais. Um terceiro corpo, também de massa [tex3]m[/tex3] , é suspenso no ponto médio M do fio e baixado até a posição de equilíbrio.
O afastamento do ponto M em relação à sua posição inicial é:
a) [tex3]\frac{d\sqrt{3}}{2}[/tex3]
b) [tex3]\frac{d\sqrt{3}}{3}[/tex3]
c) [tex3]\frac{d\sqrt{3}}{4}[/tex3]
d) [tex3]\frac{d\sqrt{3}}{6}[/tex3]
http://www.tutorbrasil.com.br/forum/vie ... 97&p=62169&
----------------------
Problema 155
(AFA - 2008) A figura abaixo apresenta dois corpos de massa [tex3]m[/tex3] suspensos por fios ideais que passam por roldanas também ideais. Um terceiro corpo, também de massa [tex3]m[/tex3] , é suspenso no ponto médio M do fio e baixado até a posição de equilíbrio.
O afastamento do ponto M em relação à sua posição inicial é:
a) [tex3]\frac{d\sqrt{3}}{2}[/tex3]
b) [tex3]\frac{d\sqrt{3}}{3}[/tex3]
c) [tex3]\frac{d\sqrt{3}}{4}[/tex3]
d) [tex3]\frac{d\sqrt{3}}{6}[/tex3]
Última edição: theblackmamba (Ter 11 Set, 2012 17:46). Total de 2 vezes.
"A coisa mais incompreensível do universo é que ele é compreensível"
- Albert Einstein
- Albert Einstein
Set 2012
12
16:35
Re: II Maratona de Física IME/ITA
Solução do Problema 155
Sendo [tex3]R_1[/tex3] , a roldana da esquerda, [tex3]R_2[/tex3] a roldana da direita, temos que:
Como as três massas são iguais, o ângulo [tex3]R_1MR_2[/tex3] , vale [tex3]120^o[/tex3] .
Dividindo esse ângulo por [tex3]2[/tex3] , temos que esse ângulo pertence a um triângulo de catetos [tex3]\frac{d}{2}[/tex3] e [tex3]h[/tex3] .
[tex3]tg \, 60^0 = \frac{\frac{d}{2}}{h}[/tex3]
[tex3]\sqrt{3} = \frac{\frac{d}{2}}{h}[/tex3]
[tex3]h = \frac{d\sqrt{3}}{6}[/tex3]
Letra D.
------------------------------------------------------------------------------------------------
Problema 156
(ITA-2001) Uma partícula, partindo do repouso, percorre no intervalo de tempo [tex3]t[/tex3] , uma distância [tex3]d[/tex3] . Nos intervalos de tempo seguintes, todos iguais a [tex3]t[/tex3] , as respectivas distâncias percorridas são iguais a [tex3]3D[/tex3] , [tex3]5D[/tex3] , [tex3]7D[/tex3] , etc. A respeito desse movimento pode-se afirmar que:
a) a distância da partícula desde o ponto em que inicia seu movimento cresce exponencialmente com o tempo.
b) a velocidade da partícula cresce exponencialmente com o tempo.
c) a distância da partícula desde o ponto em que inicia seu movimento é diretamente proporcional ao tempo elevado ao quadrado.
d) a velocidade da partícula é diretamente proporcional ao tempo elevado ao quadrado.
e) nenhuma das opções acima é correta.
Sendo [tex3]R_1[/tex3] , a roldana da esquerda, [tex3]R_2[/tex3] a roldana da direita, temos que:
Como as três massas são iguais, o ângulo [tex3]R_1MR_2[/tex3] , vale [tex3]120^o[/tex3] .
Dividindo esse ângulo por [tex3]2[/tex3] , temos que esse ângulo pertence a um triângulo de catetos [tex3]\frac{d}{2}[/tex3] e [tex3]h[/tex3] .
[tex3]tg \, 60^0 = \frac{\frac{d}{2}}{h}[/tex3]
[tex3]\sqrt{3} = \frac{\frac{d}{2}}{h}[/tex3]
[tex3]h = \frac{d\sqrt{3}}{6}[/tex3]
Letra D.
------------------------------------------------------------------------------------------------
Problema 156
(ITA-2001) Uma partícula, partindo do repouso, percorre no intervalo de tempo [tex3]t[/tex3] , uma distância [tex3]d[/tex3] . Nos intervalos de tempo seguintes, todos iguais a [tex3]t[/tex3] , as respectivas distâncias percorridas são iguais a [tex3]3D[/tex3] , [tex3]5D[/tex3] , [tex3]7D[/tex3] , etc. A respeito desse movimento pode-se afirmar que:
a) a distância da partícula desde o ponto em que inicia seu movimento cresce exponencialmente com o tempo.
b) a velocidade da partícula cresce exponencialmente com o tempo.
c) a distância da partícula desde o ponto em que inicia seu movimento é diretamente proporcional ao tempo elevado ao quadrado.
d) a velocidade da partícula é diretamente proporcional ao tempo elevado ao quadrado.
e) nenhuma das opções acima é correta.
Última edição: felps (Qua 12 Set, 2012 16:35). Total de 2 vezes.
"É melhor lançar-se à luta em busca do triunfo,mesmo expondo-se ao insucesso,do que ficar na fila dos pobres de espírito,que nem gozam muito nem sofrem muito,por viverem nessa penumbra cinzenta de não conhecer vitória e nem derrota" F. Roosevelt
-
FilipeCaceres

- Mensagens: 2504
- Registrado em: Seg 16 Nov, 2009 20:47
- Última visita: 24-01-20
Set 2012
12
21:56
Re: II Maratona de Física IME/ITA
Solução do Problema 156
Sabemos que
[tex3]S=S_0+V_0t+\frac{1}{2}at^2[/tex3]
Mas como parte do repouso [tex3](v_0=0\,m/s)[/tex3] , temos que
[tex3]\Delta S=\frac{1}{2}at^2[/tex3]
Ou seja, a distância PERCORRIDA da partícula desde o ponto em que inicia seu movimento é diretamente proporcional ao tempo elevado ao quadrado.
Sendo assim ficamos com a Letra E.
---------------------------------------------------
Problema 157
(EFOMM - 2007) Um toroide, no circuito de uma das repetidoras de radar do passadiço tem uma seção reta quadrada de lado igual a [tex3]8\,cm[/tex3] , raio interno de [tex3]18\, cm[/tex3] , [tex3]400[/tex3] espiras e é atravessado por uma corrente de intensidade igual a [tex3]0,8\, A[/tex3] . O valor aproximado do fluxo magnético através da seção reta do toroide, em microwebers, é de aproximadamente:
Dado: [tex3]\mu_0= 4\pi \times 10^{-7}[/tex3] , em unidades do S.I.
a) 2,056
b) 3,074
c) 5,022
d) 6,034
e) 8,012
Sabemos que
[tex3]S=S_0+V_0t+\frac{1}{2}at^2[/tex3]
Mas como parte do repouso [tex3](v_0=0\,m/s)[/tex3] , temos que
[tex3]\Delta S=\frac{1}{2}at^2[/tex3]
Ou seja, a distância PERCORRIDA da partícula desde o ponto em que inicia seu movimento é diretamente proporcional ao tempo elevado ao quadrado.
Sendo assim ficamos com a Letra E.
---------------------------------------------------
Problema 157
(EFOMM - 2007) Um toroide, no circuito de uma das repetidoras de radar do passadiço tem uma seção reta quadrada de lado igual a [tex3]8\,cm[/tex3] , raio interno de [tex3]18\, cm[/tex3] , [tex3]400[/tex3] espiras e é atravessado por uma corrente de intensidade igual a [tex3]0,8\, A[/tex3] . O valor aproximado do fluxo magnético através da seção reta do toroide, em microwebers, é de aproximadamente:
Dado: [tex3]\mu_0= 4\pi \times 10^{-7}[/tex3] , em unidades do S.I.
a) 2,056
b) 3,074
c) 5,022
d) 6,034
e) 8,012
Última edição: FilipeCaceres (Qua 12 Set, 2012 21:56). Total de 2 vezes.
Set 2012
13
16:13
Re: II Maratona de Física IME/ITA
Questão Anulada!
Essa questão da efomm foi anulada do concurso por exigir conceitos
avançados de cálculo integral e ainda não conter a resposta certa (1,884 microwebers)
---------
Problema 158
(ITA-2012) Considere as seguintes afirmações:
I. As energias do átomo de Hidrogênio do modelo de Bohr satisfazem à relação, [tex3]E_n=-13,6/n^2\,\,eV[/tex3] , com
n = 1, 2, 3, · · ·; portanto, o elétron no estado fundamental do átomo de Hidrogênio pode absorver
energia menor que 13,6 eV.
II. Não existe um limiar de frequência de radiação no efeito fotoelétrico.
III. O modelo de Bohr, que resulta em energias quantizadas, viola o princípio da incerteza de Heisenberg.
Então, pode-se afirmar que
a) apenas a II é incorreta.
b) apenas a I e II são corretas.
c) apenas a I e III são incorretas.
d) apenas a I é incorreta.
e) todas são incorretas.
Essa questão da efomm foi anulada do concurso por exigir conceitos
avançados de cálculo integral e ainda não conter a resposta certa (1,884 microwebers)
---------
Problema 158
(ITA-2012) Considere as seguintes afirmações:
I. As energias do átomo de Hidrogênio do modelo de Bohr satisfazem à relação, [tex3]E_n=-13,6/n^2\,\,eV[/tex3] , com
n = 1, 2, 3, · · ·; portanto, o elétron no estado fundamental do átomo de Hidrogênio pode absorver
energia menor que 13,6 eV.
II. Não existe um limiar de frequência de radiação no efeito fotoelétrico.
III. O modelo de Bohr, que resulta em energias quantizadas, viola o princípio da incerteza de Heisenberg.
Então, pode-se afirmar que
a) apenas a II é incorreta.
b) apenas a I e II são corretas.
c) apenas a I e III são incorretas.
d) apenas a I é incorreta.
e) todas são incorretas.
Última edição: Radius (Qui 13 Set, 2012 16:13). Total de 2 vezes.
-
theblackmamba

- Mensagens: 3723
- Registrado em: Ter 23 Ago, 2011 15:43
- Última visita: 20-11-19
- Localização: São Paulo - SP
Set 2012
15
08:12
Re: II Maratona de Física IME/ITA
Solução do Problema 158
(I): Correta:
Para [tex3]n=1\,\,\Rightarrow \,\,E=-13,6\,\text{eV}[/tex3]
Para [tex3]n=2\,\,\Rightarrow \,\,E=-3,40\,\text{eV}[/tex3]
Logo para o elétron dar um salto para o segundo estado excitado recebeu uma energia de [tex3]\Delta E=-3,40-(-13,6)=10,2\,\text{eV}\,\,<\,\,13,6\,\text{eV}[/tex3] .
(II): Incorreta:
De acordo com a Teoria de Einstein existe para qualquer superfície metálica um limiar de frequência denominado [tex3]f_0[/tex3] , ou seja, para frequências menores que [tex3]f_0[/tex3] o efeito não ocorre, independente da intensidade luminosa.
(III): Correta:
Bohr define em seu modelo exatamente como é a trajetória do elétron, indicando seu momento angular, que é sempre múltiplo de [tex3]\frac{h}{2\pi}[/tex3] .
Diferente de Heinsberg, o qual diz que não é possível determinar ao mesmo tempo calcular as componentes do momento e suas coordenadas.
-------------------------
Problema 159
(AFA - 2010) Uma esfera de massa [tex3]m[/tex3] , eletrizada positivamente com carga [tex3]q[/tex3] , está fixada na extremidade de um fio ideal e isolante de comprimento [tex3]\ell[/tex3] . O pêndulo, assim constituído, está imerso em uma região onde além do campo gravitacional [tex3]g[/tex3] atua um campo elétrico horizontal e uniforme [tex3]E[/tex3] . Este pêndulo é abandonado do ponto A e faz um ângulo [tex3]\theta[/tex3] com a vertical conforme mostra a figura.
Desprezando-se quaisquer resistências, ao passar pelo ponto B, simétrico de A em relação à vertical, sua energia cinética vale:
a) [tex3]2qE\ell \sen\theta[/tex3]
b) [tex3]\ell(mg+qE\sen\theta)[/tex3]
c) [tex3]2\ell(mg\cos\theta+qE\sen\theta)[/tex3]
d) [tex3]qE\ell \cos\theta[/tex3]
(I): Correta:
Para [tex3]n=1\,\,\Rightarrow \,\,E=-13,6\,\text{eV}[/tex3]
Para [tex3]n=2\,\,\Rightarrow \,\,E=-3,40\,\text{eV}[/tex3]
Logo para o elétron dar um salto para o segundo estado excitado recebeu uma energia de [tex3]\Delta E=-3,40-(-13,6)=10,2\,\text{eV}\,\,<\,\,13,6\,\text{eV}[/tex3] .
(II): Incorreta:
De acordo com a Teoria de Einstein existe para qualquer superfície metálica um limiar de frequência denominado [tex3]f_0[/tex3] , ou seja, para frequências menores que [tex3]f_0[/tex3] o efeito não ocorre, independente da intensidade luminosa.
(III): Correta:
Bohr define em seu modelo exatamente como é a trajetória do elétron, indicando seu momento angular, que é sempre múltiplo de [tex3]\frac{h}{2\pi}[/tex3] .
Diferente de Heinsberg, o qual diz que não é possível determinar ao mesmo tempo calcular as componentes do momento e suas coordenadas.
-------------------------
Problema 159
(AFA - 2010) Uma esfera de massa [tex3]m[/tex3] , eletrizada positivamente com carga [tex3]q[/tex3] , está fixada na extremidade de um fio ideal e isolante de comprimento [tex3]\ell[/tex3] . O pêndulo, assim constituído, está imerso em uma região onde além do campo gravitacional [tex3]g[/tex3] atua um campo elétrico horizontal e uniforme [tex3]E[/tex3] . Este pêndulo é abandonado do ponto A e faz um ângulo [tex3]\theta[/tex3] com a vertical conforme mostra a figura.
Desprezando-se quaisquer resistências, ao passar pelo ponto B, simétrico de A em relação à vertical, sua energia cinética vale:
a) [tex3]2qE\ell \sen\theta[/tex3]
b) [tex3]\ell(mg+qE\sen\theta)[/tex3]
c) [tex3]2\ell(mg\cos\theta+qE\sen\theta)[/tex3]
d) [tex3]qE\ell \cos\theta[/tex3]
Última edição: theblackmamba (Sáb 15 Set, 2012 08:12). Total de 2 vezes.
"A coisa mais incompreensível do universo é que ele é compreensível"
- Albert Einstein
- Albert Einstein
-
FilipeCaceres

- Mensagens: 2504
- Registrado em: Seg 16 Nov, 2009 20:47
- Última visita: 24-01-20
Set 2012
20
16:51
Re: II Maratona de Física IME/ITA
Solução do Problema 159
O único que realiza trabalho é a força elétrica, pois a tração é perpendicular ao movimento e como não temos variação de altura o força peso também não realiza trabalho.
Assim temos,
[tex3]T_r=\Delta Ec[/tex3]
[tex3]Fel\cdot d=Ec_f-Ec_i[/tex3]
[tex3]q\cdot E\cdot 2\ell\sen \theta=Ec_f-0[/tex3]
Portanto,
[tex3]\boxed{Ec_f=2q\cdot E \ell\sen \theta}[/tex3] . Letra A
----------------------------------------------------------------
Problema 160
(AFA - 2002) Considere um corpo em movimento uniform numa trajetória circular de raio [tex3]8m[/tex3] . Sabe-se que, entre os instantes [tex3]5s[/tex3] e [tex3]8s[/tex3] , e descreve um arco de comprimento [tex3]6m[/tex3] . O período do movimento do corpo, em segundos, é
a) [tex3]2\pi[/tex3]
b) [tex3]3\pi[/tex3]
c) [tex3]6\pi[/tex3]
d) [tex3]8\pi[/tex3]
O único que realiza trabalho é a força elétrica, pois a tração é perpendicular ao movimento e como não temos variação de altura o força peso também não realiza trabalho.
Assim temos,
[tex3]T_r=\Delta Ec[/tex3]
[tex3]Fel\cdot d=Ec_f-Ec_i[/tex3]
[tex3]q\cdot E\cdot 2\ell\sen \theta=Ec_f-0[/tex3]
Portanto,
[tex3]\boxed{Ec_f=2q\cdot E \ell\sen \theta}[/tex3] . Letra A
----------------------------------------------------------------
Problema 160
(AFA - 2002) Considere um corpo em movimento uniform numa trajetória circular de raio [tex3]8m[/tex3] . Sabe-se que, entre os instantes [tex3]5s[/tex3] e [tex3]8s[/tex3] , e descreve um arco de comprimento [tex3]6m[/tex3] . O período do movimento do corpo, em segundos, é
a) [tex3]2\pi[/tex3]
b) [tex3]3\pi[/tex3]
c) [tex3]6\pi[/tex3]
d) [tex3]8\pi[/tex3]
Última edição: FilipeCaceres (Qui 20 Set, 2012 16:51). Total de 2 vezes.
-
theblackmamba

- Mensagens: 3723
- Registrado em: Ter 23 Ago, 2011 15:43
- Última visita: 20-11-19
- Localização: São Paulo - SP
Set 2012
20
17:15
Re: II Maratona de Física IME/ITA
Solução do Problema 160
[tex3]v=\frac{\Delta S}{\Delta t}=\frac{6}{8-5}=2m/s[/tex3]
Mas também,
[tex3]v=\frac{2\pi r}{T}[/tex3]
[tex3]T=\frac{2\pi \cdot 8}{2}[/tex3]
[tex3]\boxed{T=8\pi\,\,\text{s}}[/tex3] . Letra D
------------------
Problema 161
(ITA - 1999) Duas esferas metálicas homogêneas de raios [tex3]r[/tex3] e [tex3]r'[/tex3] e massas específicas [tex3]5[/tex3] e [tex3]10g/cm^3[/tex3] , respetivamente têm peso [tex3]P[/tex3] no vácuo. As esferas são colocadas nas extremidades de uma alavanca e o sistema todo mergulhado em água, como mostra a figura adiante. A razão entre os dois braços da alavanca [tex3]\frac{L}{L'}[/tex3] para que haja equilíbrio é igual a :
a) 1/2
b) 9/4
c) 9/8
d) 1
e) 9/2
[tex3]v=\frac{\Delta S}{\Delta t}=\frac{6}{8-5}=2m/s[/tex3]
Mas também,
[tex3]v=\frac{2\pi r}{T}[/tex3]
[tex3]T=\frac{2\pi \cdot 8}{2}[/tex3]
[tex3]\boxed{T=8\pi\,\,\text{s}}[/tex3] . Letra D
------------------
Problema 161
(ITA - 1999) Duas esferas metálicas homogêneas de raios [tex3]r[/tex3] e [tex3]r'[/tex3] e massas específicas [tex3]5[/tex3] e [tex3]10g/cm^3[/tex3] , respetivamente têm peso [tex3]P[/tex3] no vácuo. As esferas são colocadas nas extremidades de uma alavanca e o sistema todo mergulhado em água, como mostra a figura adiante. A razão entre os dois braços da alavanca [tex3]\frac{L}{L'}[/tex3] para que haja equilíbrio é igual a :
a) 1/2
b) 9/4
c) 9/8
d) 1
e) 9/2
Última edição: theblackmamba (Qui 20 Set, 2012 17:15). Total de 2 vezes.
"A coisa mais incompreensível do universo é que ele é compreensível"
- Albert Einstein
- Albert Einstein
-
FilipeCaceres

- Mensagens: 2504
- Registrado em: Seg 16 Nov, 2009 20:47
- Última visita: 24-01-20
Set 2012
20
18:18
Re: II Maratona de Física IME/ITA
Solução do Problema 161
Esfera da direita
[tex3]P_{R1}=P'-E'=gV'(\mu_c-\mu_l)=g\frac{m}{\mu_c}(\mu_c-\mu_l)=P\left(1-\frac{\mu_l}{\mu_c}\right)[/tex3]
Esfera da esquerda
[tex3]P_{R2}=P-E=P\left(1-\frac{\mu_l}{\mu_c}\right)[/tex3]
Assim temos,
[tex3]P_{R2}\cdot L=P_{R1}\cdot L'[/tex3]
[tex3]P\left(1-\frac{\mu_l}{\mu_c}\right)\cdot L=P\left(1-\frac{\mu_l}{\mu_c}\right)\cdot L'[/tex3]
[tex3]\left(1-\frac{1}{5}\right)\cdot L=\left(1-\frac{1}{10}\right)\cdot L'[/tex3]
[tex3]\boxed{\frac{L}{L'}=\frac{9}{8}}[/tex3] . Letra C
----------------------------------------------------------
Problema 162
(AFA - 2002) Uma bola de barracha é lançada verticalmente para baixo com energia cinética [tex3]k_1[/tex3] , a partir de uma altura [tex3]h[/tex3] . Após colidir elasticamente com o solo, a bola desloca-se para cima atingindo um ponto cuja altura é [tex3]25\%[/tex3] maior que a posição inicial. Considere [tex3]k_2[/tex3] a energia cinética da bola imediatamente antes de chocar-se com o solo e calcule a razão [tex3]\frac{k_2}{k_2}[/tex3] . Despreze a resistência do ar.
a) 0,25
b) 0,20
s) 0,75
d) 1,25
Esfera da direita
[tex3]P_{R1}=P'-E'=gV'(\mu_c-\mu_l)=g\frac{m}{\mu_c}(\mu_c-\mu_l)=P\left(1-\frac{\mu_l}{\mu_c}\right)[/tex3]
Esfera da esquerda
[tex3]P_{R2}=P-E=P\left(1-\frac{\mu_l}{\mu_c}\right)[/tex3]
Assim temos,
[tex3]P_{R2}\cdot L=P_{R1}\cdot L'[/tex3]
[tex3]P\left(1-\frac{\mu_l}{\mu_c}\right)\cdot L=P\left(1-\frac{\mu_l}{\mu_c}\right)\cdot L'[/tex3]
[tex3]\left(1-\frac{1}{5}\right)\cdot L=\left(1-\frac{1}{10}\right)\cdot L'[/tex3]
[tex3]\boxed{\frac{L}{L'}=\frac{9}{8}}[/tex3] . Letra C
----------------------------------------------------------
Problema 162
(AFA - 2002) Uma bola de barracha é lançada verticalmente para baixo com energia cinética [tex3]k_1[/tex3] , a partir de uma altura [tex3]h[/tex3] . Após colidir elasticamente com o solo, a bola desloca-se para cima atingindo um ponto cuja altura é [tex3]25\%[/tex3] maior que a posição inicial. Considere [tex3]k_2[/tex3] a energia cinética da bola imediatamente antes de chocar-se com o solo e calcule a razão [tex3]\frac{k_2}{k_2}[/tex3] . Despreze a resistência do ar.
a) 0,25
b) 0,20
s) 0,75
d) 1,25
Última edição: FilipeCaceres (Qui 20 Set, 2012 18:18). Total de 2 vezes.
-
gabrielbpf

- Mensagens: 344
- Registrado em: Qui 28 Jun, 2012 00:42
- Última visita: 22-11-16
Set 2012
21
12:18
Re: II Maratona de Física IME/ITA
Solução do Problema 162
Altura inicial:
Altura final: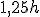
 , antes da colisão.
, antes da colisão.
Imediatamente antes de colidir com o solo, a energia mecânica é apenas cinética... Como a colisão é elástica, não se perde energia nenhuma!
Assim, na altura máxima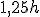 , a energia potencial será igual à cinética no chão:
, a energia potencial será igual à cinética no chão: 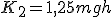 . Essa energia é a própria mecânica!
. Essa energia é a própria mecânica!
Assim:
Considerando que a questão pede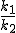 , e não
, e não 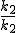 , como digitado acima, teremos a resposta:
, como digitado acima, teremos a resposta: 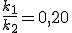
____________________________________
Problema 163
(ITA-2012) Um corpo movimenta-se numa superfície
horizontal sem atrito, a partir do repouso, devido à ação
contínua de um dispositivo que lhe fornece uma potência
mecânica constante. Sendo sua velocidade após certo
sua velocidade após certo
tempo , pode-se afirmar que
, pode-se afirmar que
A ( ) a aceleração do corpo é constante.
B ( ) a distância percorrida é proporcional a
C ( ) o quadrado da velocidade é proporcional a t.
D ( ) a força que atua sobre o corpo é proporcional a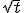 .
.
E ( ) a taxa de variação temporal de energia cinética não
é constante
Altura inicial:
Altura final:
Imediatamente antes de colidir com o solo, a energia mecânica é apenas cinética... Como a colisão é elástica, não se perde energia nenhuma!
Assim, na altura máxima
Assim:
Considerando que a questão pede
____________________________________
Problema 163
(ITA-2012) Um corpo movimenta-se numa superfície
horizontal sem atrito, a partir do repouso, devido à ação
contínua de um dispositivo que lhe fornece uma potência
mecânica constante. Sendo
tempo
A ( ) a aceleração do corpo é constante.
B ( ) a distância percorrida é proporcional a
C ( ) o quadrado da velocidade é proporcional a t.
D ( ) a força que atua sobre o corpo é proporcional a
E ( ) a taxa de variação temporal de energia cinética não
é constante
Última edição: gabrielbpf (Sex 21 Set, 2012 12:18). Total de 1 vez.
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última msg
-
- 0 Respostas
- 977 Exibições
-
Última msg por leozitz
-
- 0 Respostas
- 1539 Exibições
-
Última msg por EinsteinGenio
-
- 0 Respostas
- 707 Exibições
-
Última msg por Miquéias
-
- 1 Respostas
- 1976 Exibições
-
Última msg por guila100
-
- 3 Respostas
- 1554 Exibições
-
Última msg por luccaz1








