Ensino Médio ⇒ Geometria Plana - Área da região hachurada Tópico resolvido

[joaovitor]

Na figura, [tex3]ABCD[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]ABCD[/tex3]

é um quadrado de área igual a 225 cm², [tex3]E[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]E[/tex3]

é o ponto de interseção entre a diagonal [tex3]BD[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]BD[/tex3]

e o semicírculo de diâmetro [tex3]AD[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]AD[/tex3]

, e o segmento [tex3]CF[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]CF[/tex3]

é tangente ao semicírculo. Sabendo-se dessas informações, qual é a área do triângulo hachurado formado pelos pontos [tex3]DEF[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]DEF[/tex3]

?

Resposta

---

22,5 cm²

[DanielDC]

Vamos usar geometria analítica para resolver essa questão. Vou partir do pressuposto que você esteja familiarizado com equações de circunferência e interseção de circunferências.

Coloque o ponto A sobre a origem (0,0) e acompanhe o raciocínio. Devemos achar as coordenadas dos pontos D, E e F, em seguida usar a fórmula que calcula a área do triângulo delimitado por esses três pontos. Dois desses pontos já temos, note que temos [tex3]D(15,0)[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]D(15,0)[/tex3]

, [tex3]E(\frac{15}{2}, \frac{15}{2})[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]E(\frac{15}{2}, \frac{15}{2})[/tex3]

, falta descobrir o ponto F. Agora observe que temos a semicircunferência de diâmetro AD em que a equação da circunferência é [tex3](x-\frac{15}{2})^2+y^2=(\frac{15}{2})^2\implies x^2+y^2-15x=0.[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](x-\frac{15}{2})^2+y^2=(\frac{15}{2})^2\implies x^2+y^2-15x=0.[/tex3]

Agora observe que, de geometria, sabemos que a distância CD é a mesma da distância CF. Logo, para encontrarmos o ponto F, precisamos fazer a interseção da circunferência anterior com a circunferência de raio 15 centrada em C, note que a equação dessa circunferência é [tex3](x-15)^2+(y-15)^2=15^2[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](x-15)^2+(y-15)^2=15^2[/tex3]

. Observe a figura abaixo (os pontos estão diferentes da figura do enunciado).

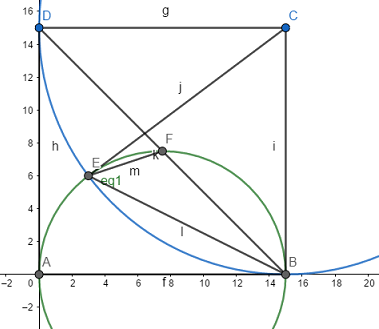
geoan.png (30 KiB) Exibido 1663 vezes

Agora, basta resolver o seguinte sistema de equações:

[tex3]\begin{cases}
x^2+y^2-15x=0 \\
(x-15)^2+(y-15)^2=15^2
\end{cases}[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]\begin{cases}
x^2+y^2-15x=0 \\
(x-15)^2+(y-15)^2=15^2
\end{cases}[/tex3]

Rapidamente esse sistema é resolvido e você achara que os pontos que satisfazem a interseção são [tex3](3,6)[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](3,6)[/tex3]

e [tex3](15,0)[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](15,0)[/tex3]

(já conhecido na figura.

Agora, basta calcular a área do triângulo delimitado pelos pontos [tex3](3,6)[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](3,6)[/tex3]

, [tex3](\frac{15}{2}, \frac{15}{2})[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](\frac{15}{2}, \frac{15}{2})[/tex3]

e [tex3](15,0)[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3](15,0)[/tex3]

.

Devemos calcular o determinante da matriz abaixo e em seguida dividir por 2.
[tex3]\frac{1}{2}\Big|D\begin{pmatrix}
3 & 6 & 1 \\
\frac{15}{2} & \frac{15}{2} & 1 \\
15 & 0 & 1 \\
\end{pmatrix}\Big|=22,5[/tex3]

Código: Selecionar tudoSHIFT+Click na eq = ZOOM

[tex3]\frac{1}{2}\Big|D\begin{pmatrix}
3 & 6 & 1 \\
\frac{15}{2} & \frac{15}{2} & 1 \\
15 & 0 & 1 \\
\end{pmatrix}\Big|=22,5[/tex3]

.

[joaovitor]

Daniel, muito obrigado por postar sua resolução via geometria analítica. Apesar de não ser uma matéria que eu vi muitas coisas a fundo, sua resolução continua sendo de grande valia. De qualquer forma, eu agradeço, pois, quando eu terminar o Fundamentos do Iezzi (de Geometria plana), provavelmente eu iniciarei com o de analítica ou espacial. Enfim, valeu demais.Tmj