Demonstração - modelo atômico de Bohr
Enviado: Sex 27 Jul, 2012 02:10
------------------------------------------------------------------------------
Hipótese:
Considere um átomo de hidrogênio representado abaixo. Sendo
, 
, 
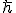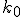e 
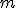a carga elétrica elementar, o momento angular do elétron, a constante eletrostática do vácuo e a massa do elétron.
Mostre que o raio de Bohr (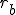
) e a energia mecânica (
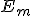) do elétron são dados por:
e  "E_{m} \, = \, - \, \frac{m \cdot k_{0}^{2} \cdot e^{4}}{2 \cdot \hbar^{2}} \cdot \left(\frac{1}{n}\right)")
onde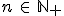 
.
-------------------------------------------------------------------------------
Demonstração:
A força de atração eletrostática é a resultante centrípeta. Nesse caso, podemos fazer
 "F_{e} \, = \, \frac{m \cdot v^{2}}{r_{b}} \,\,\, \Rightarrow \,\,\, k_{0} \cdot \frac{e^{2}}{r_{b}^{2}} \, = \, \frac{m \cdot v^{2}}{r_{b}} \,\,\, \Rightarrow \,\,\, k_{0} \cdot \frac{e^{2}}{r_{b}} \, = \, m \cdot v^{2} \,\,\, (I)")
Da definição de momento angular de uma partícula elementar em um raio de Bohr, tiramos:
 "m \cdot v \cdot r_{b} \, = \, \hbar \,\,\, \Rightarrow \,\,\, v \, = \, \frac{\hbar}{m \cdot r_{b}} \,\,\, (II)")
Substituindo "(II)")
em  "(I)")
, encontramos:
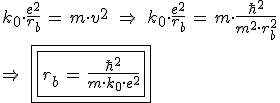
A energia mecânica total do elétron em uma orbital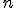
qualquer é dada por:
%7D%7Br_%7Bn%7D%7D%20%5C,%5C,%5C,%5C,%5C,%5C,%5C,%20(III) "E_{m} \, = \, E_{c} \, + \, E_{p} \,\,\, \Rightarrow \,\,\, E_{m} \, = \, \frac{m \cdot v^{2}}{2} \, + \, k_{0} \cdot \frac{e \cdot \left(- \, e\right)}{r_{n}} \,\,\,\,\,\,\, (III)")
De e  "(III)")
, tiramos:
 "E_{m} \, = \, \frac{k_{0} \cdot e^{2}}{2 \cdot r_{n}} \, - \, \frac{k_{0} \cdot e^{2}}{ r_{n}} \,\,\, \Rightarrow \,\,\, E_{m} \, = \, - \, \frac{k_{0} \cdot e^{2}}{2 \cdot r_{n}} \,\,\,\,\, (IV)")
Conforme os postulados de Bohr, temos:
%5C,%5C,%5C,%5C,%5C,%5C,%5C,%20(V) "r_{n} \, = \, n^{2} \cdot r_{b} \,\,\, \left(n \, \in \, \mathbb{N}_{+}\right)\,\,\,\,\,\,\, (V)")
De "(V)")
e  "(IV)")
, tiramos:
 "E_{m} \, = \, - \, \frac{k_{0} \cdot e^{2}}{2 \cdot r_{n}} \,\,\, \Rightarrow \,\,\, E_{m} \, = \, - \, \frac{k_{0} \cdot e^{2}}{2 \cdot r_{b}} \cdot \left(\frac{1}{n^{2}}\right)")
Substituindo o valor de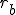 encontrado na expressão acima, vem:
%5Cleft(%5Cfrac%7B1%7D%7Bn%5E%7B2%7D%7D%5Cright)%20%5C,%5C,%5C,%20%5CRightarrow%20%5C,%5C,%5C,%20%5Cboxed%7B%5Cboxed%7B%20E_%7Bm%7D%20%5C,%20=%20%5C,%20-%20%5C,%20%5Cfrac%7Bm%20%5Ccdot%20k_%7B0%7D%5E%7B2%7D%20%5Ccdot%20e%5E%7B4%7D%7D%7B2%20%5Ccdot%20%5Chbar%5E%7B2%7D%7D%20%5Ccdot%20%5Cleft(%5Cfrac%7B1%7D%7Bn%7D%5Cright)%7D%7D "E_{m} \, = \, - \, \frac{k_{0} \cdot e^{2}}{2 } \cdot \left(\frac{m \cdot k_{0} \cdot e^{2}}{\hbar^{2}}\right)\left(\frac{1}{n^{2}}\right) \,\,\, \Rightarrow \,\,\, \boxed{\boxed{ E_{m} \, = \, - \, \frac{m \cdot k_{0}^{2} \cdot e^{4}}{2 \cdot \hbar^{2}} \cdot \left(\frac{1}{n}\right)}}")
Essa foi uma forma que eu criei de demonstrar os postulados de Bohr sem utilizar mecânica estatística.
Espero que gostem!
Hipótese:
Considere um átomo de hidrogênio representado abaixo. Sendo
- Demonstração 3.JPG (6.2 KiB) Exibido 4024 vezes
-------------------------------------------------------------------------------
Demonstração:
A força de atração eletrostática é a resultante centrípeta. Nesse caso, podemos fazer
- Demosntração 3.1.JPG (5.56 KiB) Exibido 4024 vezes
Da definição de momento angular de uma partícula elementar em um raio de Bohr, tiramos:
Substituindo
A energia mecânica total do elétron em uma orbital
De
Conforme os postulados de Bohr, temos:
De
Substituindo o valor de
Essa foi uma forma que eu criei de demonstrar os postulados de Bohr sem utilizar mecânica estatística.
Espero que gostem!