Observe o seguinte anexo:
- abc.jpg (40.07 KiB) Exibido 931 vezes
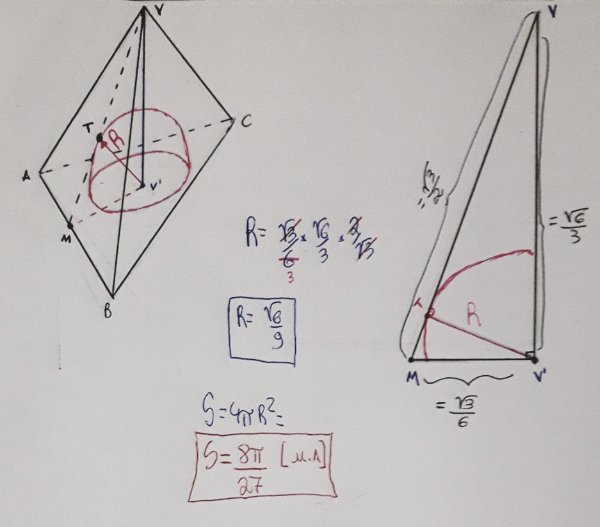
Usaremos a simetria espacial do tetraedro regular, nomeando seus vértices por [tex3]\mathsf{A, B, C, V.}[/tex3]
Seja [tex3]\mathsf{l \ = \ 1}[/tex3]
o lado do tetraedro.
Pela disposição do desenho, [tex3]\mathsf{V}[/tex3]
é o vértice mais acima, e dele desenhamos a sua projeção na face [tex3]\mathsf{\triangle ABC}[/tex3]
como sendo [tex3]\mathsf{V'. \ \overline{VV'}}[/tex3]
é altura do tetraedro.
Sendo a face [tex3]\mathsf{\triangle ABV}[/tex3]
equilátera, com [tex3]\mathsf{M}[/tex3]
sendo a projeção de [tex3]\mathsf{V}[/tex3]
em [tex3]\mathsf{\overline{AB}}[/tex3]
, temos que esse segmento é altura da face. Logo, [tex3]\mathsf{\overline{MV} \ = \ \dfrac{\cancelto{1}{l} \cdot \sqrt{3}}{2} \ = \ \dfrac{\sqrt{3}}{2}.}[/tex3]
Além disso, pela simetria do tetraedro, [tex3]\mathsf{V'}[/tex3]
encontra-se no centro da face [tex3]\mathsf{\triangle ABC}[/tex3]
, sendo equidistante dos lados e dos vértices dessa face. Temos então que [tex3]\mathsf{\overline{MV'}}[/tex3]
é apótema da base: [tex3]\mathsf{\overline{MV'} \ = \ \dfrac{\sqrt{3}}{6}}[/tex3]
.
Por Pitágoras, também teremos a altura do tetraedro, [tex3]\mathsf{\overline{VV'} \ = \ \dfrac{\sqrt{6}}{3}.}[/tex3]
Tendo todas essas informações, perceba que a esfera do enunciado possui tangências com todas as três "faces laterais" (na disposição do desenho), e sendo [tex3]\mathsf{T}[/tex3]
o ponto de tangência (simétrico) em [tex3]\mathsf{\triangle ABV, \overline{TV'} \ = \ R}[/tex3]
, justamente o raio dessa esfera. Isso porque [tex3]\mathsf{V'}[/tex3]
coincide com o centro da esfera, que se dispõe simetricamente pelo tetraedro.
Usando a propriedade da tangência, e destacando [tex3]\mathsf{\triangle MVV'}[/tex3]
, temos que [tex3]\mathsf{R}[/tex3]
é, neste caso, a altura relativa à hipotenusa. Logo, [tex3]\mathsf{R \ = \ \dfrac{\sqrt{6}}{9}.}[/tex3]
A área total da esfera é [tex3]\mathsf{S \ = \ 4 \cdot \pi \cdot R^2:}[/tex3]
[tex3]\boxed{\boxed{\mathsf{S \ = \ \dfrac{8 \cdot \pi}{27} \ \big[u. A.\big]}}}[/tex3]
That's all I'd do all day. I'd just be the catcher in the rye and all.
"Last year's wishes are this year's apologies... Every last time I come home (...)"
Poli-USP

