Página 1 de 1
(Escola Naval) Função Modular
Enviado: Ter 02 Jan, 2018 14:43
por Oziel
O gráfico da função :
[tex3]f(x)=\left\{\frac{|x^2-4x+3|}{x-3}+2x-1,\text{ se }x\ne3\right\}\{0,\text{ se }x=3\}[/tex3]
é :

- Grafic - EN.jpg (31.5 KiB) Exibido 1450 vezes
gab:

- gg (2).jpg (26.25 KiB) Exibido 1497 vezes
Re: Função Modular - Escola Naval
Enviado: Ter 02 Jan, 2018 20:03
por csmarcelo
Oziel, em questões de múltipla escolha, o correto é que informe todas as opções.
Re: Função Modular - Escola Naval
Enviado: Seg 08 Jan, 2018 15:27
por Oziel
Por alguma razão eu não consigo mais editar esse tópico.
Segue as alternativas :
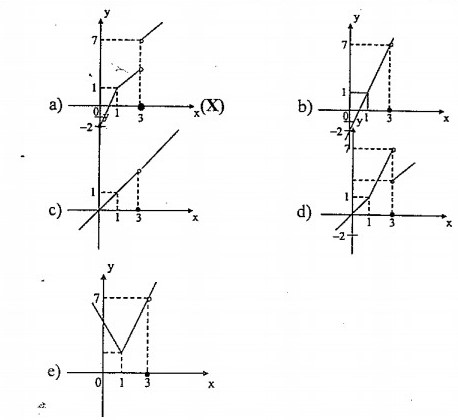
- vgg (2).jpg (49.03 KiB) Exibido 1467 vezes
Re: (Escola Naval) Função Modular
Enviado: Seg 08 Jan, 2018 21:06
por csmarcelo
[tex3]x^2-4x+3=(x-1)(x-3)[/tex3]
,
Para [tex3](x-1)(x-3)\geq0[/tex3]
, ou seja, [tex3]x\leq0[/tex3]
ou [tex3]x\geq3[/tex3]
,
[tex3]\frac{|x^2-4x+3|}{x-3}+2x-1=\frac{(x-1)(x-3)}{x-3}+2x-1=x-1+2x-1=3x-2[/tex3]
Para [tex3](x-1)(x-3)<0[/tex3]
, ou seja, [tex3]0<x<3[/tex3]
,
[tex3]\frac{|x^2-4x+3|}{x-3}+2x-1=\frac{(1-x)(x-3)}{x-3}+2x-1=1-x+2x-1=x[/tex3]
Repare que só pude cortar o denominador, pois é condição que [tex3]x\neq3[/tex3]
.
Veja agora que:
1) [tex3]\lim_{x\rightarrow3^-}x=3[/tex3]
2) [tex3]\lim_{x\rightarrow3^+}3x-2=7[/tex3]
Daí, a única opção que encaixa é a letra (a).