Aiaiaiai,esses números complexos de novo...
Considere os numeros complexos z tais que [tex3]\left|z+\frac{1}{z}\right|=1[/tex3]
.Determine o valor máximo do modulo de z.
bjos
IME / ITA ⇒ (IME/CG - 2000) Números Complexos Tópico resolvido
Moderador: [ Moderadores TTB ]
-
aline

- Mensagens: 55
- Registrado em: Sáb 21 Out, 2006 19:57
- Última visita: 02-03-23
- Localização: JF - Minas Gerais
Nov 2006
06
13:27
(IME/CG - 2000) Números Complexos
Última edição: aline (Seg 06 Nov, 2006 13:27). Total de 1 vez.
-
Daniel Hartmann

- Mensagens: 48
- Registrado em: Seg 30 Out, 2006 12:31
- Última visita: 18-03-09
- Localização: Jaciara - MT
Nov 2006
11
00:01
Re: (IME/CG - 2000) Números Complexos
Olá aline. Eu tentei resolver...
Sendo [tex3]z=a + bi[/tex3] (com [tex3]a[/tex3] e [tex3]b[/tex3] pertencentes aos reais), temos:
[tex3]\left|(a+bi) + \frac{1}{a+bi}\right|=1[/tex3]
[tex3]\left|(a+bi) + \frac{1}{a+bi}.\frac{a-bi}{a-bi}\right|=1[/tex3]
[tex3]\left|(a+bi) + \frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{(a^2+b^2).(a+bi)}{a^2+b^2}+\frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{a^3+a^2bi+ab^2+b^3i}{a^2+b^2}+\frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{a^3+ab^2+a}{a^2+b^2}+\frac{b^3i+a^2bi-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\left[\frac{a.(a^2+b^2+1)}{a^2+b^2}\right]+\left[\frac{b.(a^2+b^2-1)}{a^2+b^2}\right].i\right|=1[/tex3]
Ufa... temos então o valor do módulo de um número complexo, em função do número [tex3]z[/tex3] inicial. Se o problema pediu para considerar todos os número complexos escritos nessa forma final que possuem módulo igual a 1, veja o que nós temos (de acordo com o meu pensamento):

Então, olhando ali em cima, qual o maior ponto (que provavelmente propiciaria o maior módulo para [tex3]z[/tex3] )? Ora, é (0,1). Portanto, a parte REAL do complexo vale zero, e a parte IMAGINÁRIA vale um. De acordo com o que eu encontrei anteriormente, podemos escrever:
[tex3]\frac{a.(a^2 +b^2+1)}{a^2+b^2}=0[/tex3]
[tex3]a(a^2+b^2+1)=0[/tex3]
Aqui podemos ter:
[tex3]a^2 + b^2+1=0[/tex3] [tex3]\rightarrow[/tex3] [tex3]a^2+b^2=-1[/tex3] (o que soa a um certo absurdo, dado que a soma dos quadrados de dois números reais não pode ser negativa)
OU
[tex3]a=0[/tex3] (o que passarei a considerar)
Agora, a parte imaginária:
[tex3]\frac{b.(a^2+b^2-1)}{a^2+b^2}=1[/tex3]
Como a=0:
[tex3]\frac{b.(b^2-1)}{b^2}=1[/tex3]
[tex3]b^3-b=b^2[/tex3]
[tex3]b^3-b^2-b=0[/tex3]
[tex3]b(b^2-b-1)=0[/tex3]
Agora, podemos ter:
[tex3]b=0[/tex3] (o que também soa a absurdo, pois como [tex3]a=0[/tex3] , não teríamos um número complexo, apenas o 0, que possui módulo 0)
OU
[tex3]b^2-b-1=0[/tex3] (o que passarei a considerar)
Resolvendo essa equação, encontramos:
[tex3]b=\frac{1+\sqrt{5}}{2}[/tex3] ou [tex3]b=\frac{1-\sqrt{5}}{2}[/tex3] . Como é pedido o valor máximo do módulo de [tex3]z[/tex3] , podemos considerar que:
[tex3]z = a+bi[/tex3]
[tex3]z = \left(\frac{1+\sqrt{5}}{2}\right)i[/tex3]
O módulo desse número, então, é:
[tex3]\sqrt{\left(\frac{1+\sqrt{5}}{2}\right)^2}[/tex3] , que resulta em [tex3]\frac{1+\sqrt{5}}{2}[/tex3] (se você quiser voltar naquela figura e usar o ponto mínimo (0,-1), vai encontar o mesmo valor para o módulo de [tex3]z[/tex3] ).
UFA... Será isso mesmo?!
Até mais!
Sendo [tex3]z=a + bi[/tex3] (com [tex3]a[/tex3] e [tex3]b[/tex3] pertencentes aos reais), temos:
[tex3]\left|(a+bi) + \frac{1}{a+bi}\right|=1[/tex3]
[tex3]\left|(a+bi) + \frac{1}{a+bi}.\frac{a-bi}{a-bi}\right|=1[/tex3]
[tex3]\left|(a+bi) + \frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{(a^2+b^2).(a+bi)}{a^2+b^2}+\frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{a^3+a^2bi+ab^2+b^3i}{a^2+b^2}+\frac{a-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\frac{a^3+ab^2+a}{a^2+b^2}+\frac{b^3i+a^2bi-bi}{a^2+b^2}\right|=1[/tex3]
[tex3]\left|\left[\frac{a.(a^2+b^2+1)}{a^2+b^2}\right]+\left[\frac{b.(a^2+b^2-1)}{a^2+b^2}\right].i\right|=1[/tex3]
Ufa... temos então o valor do módulo de um número complexo, em função do número [tex3]z[/tex3] inicial. Se o problema pediu para considerar todos os número complexos escritos nessa forma final que possuem módulo igual a 1, veja o que nós temos (de acordo com o meu pensamento):

Então, olhando ali em cima, qual o maior ponto (que provavelmente propiciaria o maior módulo para [tex3]z[/tex3] )? Ora, é (0,1). Portanto, a parte REAL do complexo vale zero, e a parte IMAGINÁRIA vale um. De acordo com o que eu encontrei anteriormente, podemos escrever:
[tex3]\frac{a.(a^2 +b^2+1)}{a^2+b^2}=0[/tex3]
[tex3]a(a^2+b^2+1)=0[/tex3]
Aqui podemos ter:
[tex3]a^2 + b^2+1=0[/tex3] [tex3]\rightarrow[/tex3] [tex3]a^2+b^2=-1[/tex3] (o que soa a um certo absurdo, dado que a soma dos quadrados de dois números reais não pode ser negativa)
OU
[tex3]a=0[/tex3] (o que passarei a considerar)
Agora, a parte imaginária:
[tex3]\frac{b.(a^2+b^2-1)}{a^2+b^2}=1[/tex3]
Como a=0:
[tex3]\frac{b.(b^2-1)}{b^2}=1[/tex3]
[tex3]b^3-b=b^2[/tex3]
[tex3]b^3-b^2-b=0[/tex3]
[tex3]b(b^2-b-1)=0[/tex3]
Agora, podemos ter:
[tex3]b=0[/tex3] (o que também soa a absurdo, pois como [tex3]a=0[/tex3] , não teríamos um número complexo, apenas o 0, que possui módulo 0)
OU
[tex3]b^2-b-1=0[/tex3] (o que passarei a considerar)
Resolvendo essa equação, encontramos:
[tex3]b=\frac{1+\sqrt{5}}{2}[/tex3] ou [tex3]b=\frac{1-\sqrt{5}}{2}[/tex3] . Como é pedido o valor máximo do módulo de [tex3]z[/tex3] , podemos considerar que:
[tex3]z = a+bi[/tex3]
[tex3]z = \left(\frac{1+\sqrt{5}}{2}\right)i[/tex3]
O módulo desse número, então, é:
[tex3]\sqrt{\left(\frac{1+\sqrt{5}}{2}\right)^2}[/tex3] , que resulta em [tex3]\frac{1+\sqrt{5}}{2}[/tex3] (se você quiser voltar naquela figura e usar o ponto mínimo (0,-1), vai encontar o mesmo valor para o módulo de [tex3]z[/tex3] ).
UFA... Será isso mesmo?!
Até mais!
Última edição: Daniel Hartmann (Sáb 11 Nov, 2006 00:01). Total de 1 vez.
"Nessa história de olho por olho, dente por dente, alguém sempre acaba cego." - Ditado popular
Guia de Problemas Matemáticos - Um projeto integrante do Wikilivros.
Guia de Problemas Matemáticos - Um projeto integrante do Wikilivros.
-
bigjohn

- Mensagens: 110
- Registrado em: Seg 23 Out, 2006 22:55
- Última visita: 04-03-23
- Localização: Rio de Janeiro
Nov 2006
11
19:59
Re: (IME/CG - 2000) Números Complexos
Ae Daniel, caraca ficou grande seu post...
Cara, só não entendi pq escolher o ponto (0,1)... mas o resto está super bem explicado...
Também não consegui fazer esta questão... tou tentando...
vlw mlk
Cara, só não entendi pq escolher o ponto (0,1)... mas o resto está super bem explicado...
Também não consegui fazer esta questão... tou tentando...
vlw mlk
Última edição: bigjohn (Sáb 11 Nov, 2006 19:59). Total de 1 vez.
-
caju

- Mensagens: 2136
- Registrado em: Qui 19 Out, 2006 15:03
- Última visita: 12-04-24
- Localização: Rio de Janeiro
- Contato:
Nov 2006
13
22:35
Re: (IME/CG - 2000) Números Complexos
Olá Aline, Daniel e Bigjohn,
Como esta questão é do CG do IME, é permitido utilizar cálculo diferencial e integral, pois é parte do cronograma deste concurso. Note que falei CG e não CFG, que é o concurso no qual todos nós fazemso. CG é o concurso específico para os tenentes da Academia Agulhas Negras, que já tiveram essa matéria lá.
Bom, mas vamos lá. Começamos trocando o valor de Z por)
+%5Cfrac%7B1%7D%7B%5Crho%5Ccdot%20cis(%5Ctheta)%7D%5Cright%7C=1)
+%5Cfrac%7B1%7D%7B%5Crho%7D%5Ccdot%20(cis(%5Ctheta))%5E%7B-1%7D%5Cright%7C=1)
Agora podemos aplicar a fórmula de De Moivre para potenciação para números complexos:
+%5Cfrac%7B1%7D%7B%5Crho%7D%5Ccdot%20cis(-%5Ctheta)%5Cright%7C=1)
-%5Cfrac%7B1%7D%7B%5Crho%7D%5Ccdot%20cis(%5Ctheta)%5Cright%7C=1)
Agora devemos fazer a análise vetorial desta subtração:
Nesse gráfico representei o complexo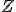 e o
e o 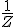
Agora é só aplicar uma lei dos co-senos no triângulo vermelho de lados 1,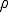 e
e 
Veja que o ângulo deste triângulo mede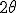 . Aplicando a lei:
. Aplicando a lei:
)
)
Devemos então achar o valor máximo de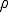 .
.
Derivando em relação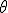
)
%7D%7B%5Crho-%5Cfrac%7B1%7D%7B%5Crho%5E3%7D%7D)
Agora igualamos a ZERO para encontrar o válor de máximo:
%7D%7B%5Crho-%5Cfrac%7B1%7D%7B%5Crho%5E3%7D%7D)
)
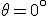
Agora voltamos para a equação original, substituímos o valor de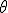 para encontrar o valor de
para encontrar o valor de 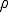 correspondente.
correspondente.
)

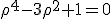
Resolvendo esta equação biquadrada encontramos o valor de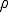 .
.
Como já está super grande este post, deixo esta equação para alguém que quiser terminar. Obrigado,
Atenciosamente
Prof. Caju
WebMaster TutorBrasil.com.br
Como esta questão é do CG do IME, é permitido utilizar cálculo diferencial e integral, pois é parte do cronograma deste concurso. Note que falei CG e não CFG, que é o concurso no qual todos nós fazemso. CG é o concurso específico para os tenentes da Academia Agulhas Negras, que já tiveram essa matéria lá.
Bom, mas vamos lá. Começamos trocando o valor de Z por
Agora podemos aplicar a fórmula de De Moivre para potenciação para números complexos:
Agora devemos fazer a análise vetorial desta subtração:
Nesse gráfico representei o complexo
Agora é só aplicar uma lei dos co-senos no triângulo vermelho de lados 1,
Veja que o ângulo deste triângulo mede
Devemos então achar o valor máximo de
Derivando em relação
Agora igualamos a ZERO para encontrar o válor de máximo:
Agora voltamos para a equação original, substituímos o valor de
Resolvendo esta equação biquadrada encontramos o valor de
Como já está super grande este post, deixo esta equação para alguém que quiser terminar. Obrigado,
Atenciosamente
Prof. Caju
WebMaster TutorBrasil.com.br
Última edição: caju (Seg 13 Nov, 2006 22:35). Total de 1 vez.
-
Daniel Hartmann

- Mensagens: 48
- Registrado em: Seg 30 Out, 2006 12:31
- Última visita: 18-03-09
- Localização: Jaciara - MT
Nov 2006
14
15:26
Re: (IME/CG - 2000) Números Complexos
Olá todo mundo! Eu tentei terminar a equação biquadrada enontrada pelo Prof. caju e encontrei o mesmo valor: [tex3]\frac{1+\sqrt{5}}{2}[/tex3]
(fatorando, mas encontrei)...
Última edição: Daniel Hartmann (Ter 14 Nov, 2006 15:26). Total de 1 vez.
"Nessa história de olho por olho, dente por dente, alguém sempre acaba cego." - Ditado popular
Guia de Problemas Matemáticos - Um projeto integrante do Wikilivros.
Guia de Problemas Matemáticos - Um projeto integrante do Wikilivros.
-
- Tópicos Semelhantes
- Respostas
- Exibições
- Última msg
-
- 1 Respostas
- 816 Exibições
-
Última msg por FelipeMartin
-
- 4 Respostas
- 10167 Exibições
-
Última msg por iammaribrg
-
- 1 Respostas
- 395 Exibições
-
Última msg por GugaSimas
-
- 1 Respostas
- 102 Exibições
-
Última msg por petras
-
- 3 Respostas
- 6144 Exibições
-
Última msg por n4ruto







