Fórum TutorBrasil - Matemática, Português, Física, Química e Biologia

Oito equipes classificaram-se para as quartas-de-final de um torneio. Um sorteio definirá duplas de equipes que se enfrentarão numa LISTA de 4 jogos.
A seguir, apresenta-se uma possível LISTA, resultado desse sorteio.

Equipe 3 x Equipe 8
Equipe 5 x Equipe 1
Equipe 4 x Equipe 2
Equipe 6 x Equipe 7

Considere que:

• o jogo descrito como Equipe A x Equipe B é o mesmo que Equipe B x Equipe A. Portanto, a ordem em que as equipes são descritas em um jogo é indiferente;
• duas listas são diferentes se pelo menos um dentre os 4 jogos é diferente.

Nessas condições, o número de diferentes LISTAS que podem ser definidas pelo sorteio é

a) 2520.
b) 1260.
c) 960.
d) 840.
e) 420.

Olá LEOMONITOR,

Tentei resolver mas não cheguei nem perto das alternativas.
Não faço ideia do que estou errando, mas vou postar aqui. Quem sabe você não encontra o erro e termina a resolução.

1) Vamos pensar nas equipes como um conjunto:
$\Omega = ({A, B, ..., G, H})$
$n(\Omega) = 8$

2) Um jogo é um subconjunto formado por 2 elementos distintos do conjunto $\Omega$ .
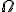
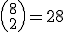
${8 \choose 2} = 28$ jogos distintos entre si.

3) Agora, vamos pensar nos jogos como um conjunto:
$\psi = ({AB, AC, ..., GH})$
$n(\psi) = 28$

4) Uma lista é um subconjunto formado por 4 elementos distintos do conjunto $\psi$ .
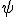
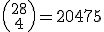
${28 \choose 4} = 20475$ listas distintas entre si.

Olá pietrotavares, eu fiz o seguinte:

Como são 4 jogos por lista, para o primeiro jogo teremos: [tex3]C_{8}^{2}[/tex3]
Para o segundo: [tex3]C_{6}^{2}[/tex3]
Para o terceiro: [tex3]C_{4}^{2}[/tex3]
Para o quarto: [tex3]C_{2}^{2}[/tex3]

Como são acontecimentos sucessivos e independentes: [tex3]C_{8}^{2}[/tex3] *[tex3]C_{6}^{2}[/tex3] *[tex3]C_{4}^{2}[/tex3] *[tex3]C_{2}^{2}[/tex3] = 2520

Não consegui chegar a outro valor, mas o gabarito oficial diz que a resposta é 420.

Eu discordo do seu item 4, pois ao escolher 4 jogos entre 28, você não garante que os quatro jogos apresentam equipes distintas, ou seja, você pode estar escolhendo (E1xE2) e (E1xE3) e a mesma equipe não pode participar de mais de um jogo na mesma lista.

Sim, percebi isso pouco antes de você responder.
Teria feito exatamente o que você fez, me parece certo.

Resta esperar alguém resolver..

Eu não sei se entendi errado o enunciado mas pra mim a resposta seria 105. Veja que a combinação apenas garante que, por exemplo, os jogos entre os times AB e BA não sejam contados como diferentes. Acontece que, fazendo o produto das combinações, listas como AB CD EF GH e AB CD GH EF são computadas como diferentes, mas eu creio que essas listas não são diferentes segundo o enunciado, já que seriam os mesmos jogos porém em outra ordem. Isso nos leva a dividir o resultado obtido por n!, sendo n o número de jogos. No caso: 2520/4!=105, mas novamente não tem resposta.

undefinied3 escreveu:Eu não sei se entendi errado o enunciado mas pra mim a resposta seria 105. Veja que a combinação apenas garante que, por exemplo, os jogos entre os times AB e BA não sejam contados como diferentes. Acontece que, fazendo o produto das combinações, listas como AB CD EF GH e AB CD GH EF são computadas como diferentes, mas eu creio que essas listas não são diferentes segundo o enunciado, já que seriam os mesmos jogos porém em outra ordem. Isso nos leva a dividir o resultado obtido por n!, sendo n o número de jogos. No caso: 2520/4!=105, mas novamente não tem resposta.

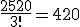
Repare que $\frac{2520}{3!} = 420$ (o suposto gabarito), não poderíamos fazer isso?
Quero dizer, tem necessidade de fazer o desprezo da ordem até pra última combinação, $({2 \choose 2} = 1)$ ), que apresenta só uma ordem possível de qualquer jeito?

Não sei se entendi exatamente o seu raciocínio, ainda estou começando na combinatória..

Eu tinha notado isso também mas não consegui justificar usar 3! em vez de 4!
A ideia é a seguinte: quando usamos a combinação pra escolher cada um dos jogos, o fato de usarmos combinação e não arranjo garante apenas a seguinte parte do enunciado:
"o jogo descrito como Equipe A x Equipe B é o mesmo que Equipe B x Equipe A. Portanto, a ordem em que as equipes são descritas em um jogo é indiferente;"
Porque combinação não difere AB e BA.
Depois, quando montamos todos os jogos (todas as combinações) e multiplicamos, é aí que começa a ser contado mais do que deveria, ao meu ver.
Utilizando novamente do meu exemplo mais reduzido com 4 times A B C D:
A primeira combinação (4 elementos escolhe 2) pode montar por exemplo o time AB e a segunda (2 elementos escolhe 2) pode montar o time CD. Teríamos a lista AB CD.
Porém, a primeira combinação pode montar o time CD e a última acabar montando o time AB, dando a lista CD AB que é a mesma lista.
No geral, pra n jogos, a gente divide por n! por causa da permutação entre da ordem dos jogos. Essa é uma das primeiras ideias que vemos na combinatória: de quantas maneiras podemos ordenar n elementos -> n! É por isso que dividimos o resultado por n!, pra que consideremos qualquer ordem desses jogos como uma única lista.

undefinied3 escreveu:Eu não sei se entendi errado o enunciado mas pra mim a resposta seria 105. Veja que a combinação apenas garante que, por exemplo, os jogos entre os times AB e BA não sejam contados como diferentes. Acontece que, fazendo o produto das combinações, listas como AB CD EF GH e AB CD GH EF são computadas como diferentes, mas eu creio que essas listas não são diferentes segundo o enunciado, já que seriam os mesmos jogos porém em outra ordem. Isso nos leva a dividir o resultado obtido por n!, sendo n o número de jogos. No caso: 2520/4!=105, mas novamente não tem resposta.

Não discordo do seu raciocínio, também cheguei a este resultado de 105. Esta questão não foi anulada pelo gabarito original da banca.

undefinied3 escreveu:Eu tinha notado isso também mas não consegui justificar usar 3! em vez de 4!
A ideia é a seguinte: quando usamos a combinação pra escolher cada um dos jogos, o fato de usarmos combinação e não arranjo garante apenas a seguinte parte do enunciado:
"o jogo descrito como Equipe A x Equipe B é o mesmo que Equipe B x Equipe A. Portanto, a ordem em que as equipes são descritas em um jogo é indiferente;"
Porque combinação não difere AB e BA.
Depois, quando montamos todos os jogos (todas as combinações) e multiplicamos, é aí que começa a ser contado mais do que deveria, ao meu ver.
Utilizando novamente do meu exemplo mais reduzido com 4 times A B C D:
A primeira combinação (4 elementos escolhe 2) pode montar por exemplo o time AB e a segunda (2 elementos escolhe 2) pode montar o time CD. Teríamos a lista AB CD.
Porém, a primeira combinação pode montar o time CD e a última acabar montando o time AB, dando a lista CD AB que é a mesma lista.
No geral, pra n jogos, a gente divide por n! por causa da permutação entre da ordem dos jogos. Essa é uma das primeiras ideias que vemos na combinatória: de quantas maneiras podemos ordenar n elementos -> n! É por isso que dividimos o resultado por n!, pra que consideremos qualquer ordem desses jogos como uma única lista.

Perfeito, mas como chegar ao 3!? Se fosse um caso de permutação circular, conseguiríamos.

Ola colegas... Essa questao pode ser resolvida por permutacao circular e repeticao da seguinte maneira:
como sao oito equipes, fixamos uma e permutamos as demais para saber o total de distribuicoes. Logo, n=8, fica:
Pn = (n-1)! = 7! = 5040.
Agora, como a ordem é indiferente, dividimos por 2! para eliminarmos a repeticao de equipes (tipo 1 e 2 e 2e 1). Logo:
5040/2! = 2520 equipes. Agora, como listas contendo 4 jogos diferentes, tiramos a repeticao de listas com os mesmos jogos em ordem diferente dividindo por 3!, ja que um jogo diferente ja caracteriza uma nova lista (por isso nao divide por 4!). logo, fica:
2520/3!= 2520/3! = 420 listas.
Resumindo:
7!/2!3!=420 listas diferentes.

Entendido?

Bons estudos.

Fórum TutorBrasil - Matemática, Português, Física, Química e Biologia

(SOUZA MARQUES - 2016) Análise Combinatória

(SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 16) ANÁLISE COMBINATÓRIA

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 16) ANÁLISE COMBINATÓRIA

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 2016) Análise Combinatória

Re: (SOUZA MARQUES - 2016) Análise Combinatória