Picolino,
Picolino escreveu: ↑Qua 10 Jan, 2024 18:43
considerei o campo induzido num ponto muito próximo internamente da superfície com sendo aproximadamente igual ao campo induzido muito proximo á superfície, mas com "sinal trocado", ou seja:
Es = 2.E
Colocando o campo resultante na direção normal:
En = 2.Ecos(x)
Sinceramente, eu não entendi o que você tentou fazer aqui. Pelo o que você escreveu, me parece que você tentou usar o fato de que, quando "vamos" do interior da esfera para o exterior, basta somarmos um termo [tex3]\frac{\sigma(\theta)}{\epsilon_0},[/tex3]
na direção radial para fora, ao campo elétrico interno para obtermos o campo elétrico externo, mas as equações que você escreveu não fazem sentido. Uma coisa que talvez tenha a ver com o seu equívoco: Lembre-se que
todas as cargas na superfície da esfera contribuem para o campo em um determinado ponto, mesmo que esse ponto esteja infinitamente próximo à superfície. Você não pode considerar apenas a contribuição das cargas muito próximas.
Esse problema da esfera metálica em um campo elétrico uniforme é bastante usual. Uma forma de resolvê-lo usando apenas eletrostática elementar é a seguinte: considere duas esferas uniformemente carregadas, com densidades de carga [tex3]\pm \rho,[/tex3]
com seus centros, O e O', separados de uma distância [tex3]a[/tex3]
muito pequena. Seja [tex3]\vec{a}=\vec{OO'}.[/tex3]

- Screenshot 2024-01-10 235625.png (42.67 KiB) Exibido 325 vezes
Para calcular o campo em um ponto dentro da interseção das duas esferas, podemos usar o fato de que o campo no interior de uma esfera homogênea de densidade de carga [tex3]\rho[/tex3]
é [tex3]\vec{E}=\frac{\rho}{3\epsilon_0}\vec{r},[/tex3]
o que pode ser facilmente mostrado com a lei de Gauss. Daí, contabilizando as contribuições das duas esferas, o campo elétrico em um ponto dentro da região de interseção é [tex3]\vec{E}=\frac{\rho}{3\epsilon_0}\vec{r_+}+\frac{-\rho}{3\epsilon_0}\vec{r_-}=\frac{\rho}{3\epsilon_0}(\vec{r_+}-\vec{r_-}),[/tex3]
onde r+ e r- são os vetores posição do ponto em relação ao centro da esfera positiva e o centro da esfera negativa, respectivamente.
Mas veja que [tex3]\vec{a}+\vec{r_+}=\vec{r_-} \Longrightarrow \vec{r_+}-\vec{r_-}=-\vec{a},[/tex3]
logo o campo elétrico dentro da interseção das esferas é constante, de módulo [tex3]E=\frac{\rho a}{3\epsilon_0}[/tex3]
e apontando para a esquerda.
Agora, considere o limite [tex3]a \rightarrow 0,[/tex3]
de modo que a região das esferas que está fora da interseção tem uma espessura infinitesimal. Podemos então, em primeira aproximação, considerar essa superfície na parte de fora da interseção como uma única esfera (daí a relevância disso para o problema original).
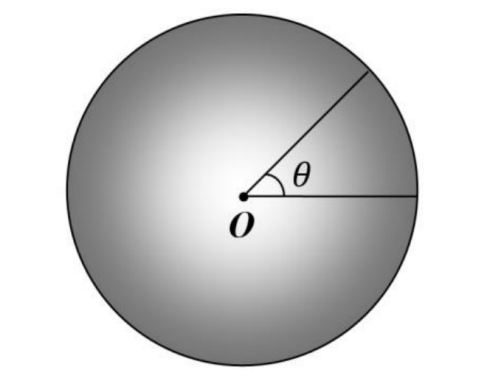
- Screenshot 2024-01-11 000834.png (62.3 KiB) Exibido 325 vezes
Imagine que traçamos dois raios, um partindo de O e outro de O', formando um ângulo [tex3]\theta[/tex3]
com a horizontal. Ao fazer isso, veja que o raio que parte de O está "atrasado" de uma distância [tex3]a \cos(\theta)[/tex3]
em relação ao raio que parte de O' (se isso não estiver claro, desenhe. É a mesma aproximação que você faz quando você resolve questões de óptica física sobre fendas). Por isso, a distância entre a superfície da esfera imaginária negativa e a da esfera imaginária positiva, para um dado [tex3]\theta,[/tex3]
é [tex3]\delta =a \cos(\theta).[/tex3]
Daí, como essa região de espessura [tex3]\delta[/tex3]
possui densidade de carga [tex3]\rho,[/tex3]
a densidade superficial de carga é [tex3]\sigma(\theta)=\rho \delta(\theta)=\rho a \cos(\theta).[/tex3]
Você pode verificar facilmente que essa equação também vale para pontos na esfera em outros quadrantes, não sendo necessário alterar nenhum sinal.
Ou seja, acabamos de achar uma função de distribuição de carga em uma superfície esférica que gera um campo elétrico uniforme dentro de si: precisamente o que queríamos. Sendo [tex3]E_0[/tex3]
o campo externo, queremos que [tex3]\frac{\rho a}{3\epsilon_0}=E_0 \Longrightarrow \rho a=3\epsilon_0 E_0,[/tex3]
e aí:
[tex3]\boxed{\sigma(\theta)=3\epsilon_0 E_0 \cos(\theta)}[/tex3]
Esse é o jeito "carteado" de resolver esse problema, que utiliza apenas conceitos básicos de eletrostática. O jeito formal de resolver o problema é usando o fato de que a equação de Laplace, [tex3]\nabla ^2 V=0,[/tex3]
possui a seguinte solução geral em sistemas com simetria axial:
[tex3]V(r, \theta)=\sum_{l=0}^{\infty}\left(A_lr^l+\frac{B_l}{r^{l+1}}\right)P_l(\cos(\theta)),[/tex3]
onde [tex3]A_l,[/tex3]
[tex3]B_l[/tex3]
são constantes e [tex3]P_l[/tex3]
é o l-ésimo polinômio de Legendre. Feito isso, usamos algumas identidades fundamentais da eletrostática e plugamos condições de contorno, chegando no mesmo resultado para [tex3]\sigma(\theta).[/tex3]










